Skillnad mellan versioner av "3.5 Lösning 6b"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (3 mellanliggande versioner av samma användare visas inte) | |||
| Rad 5: | Rad 5: | ||
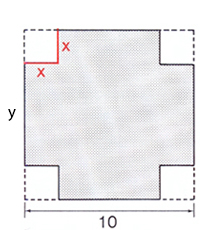
::<math> y \, = \, 10 \, - \, 2\,x \, </math> | ::<math> y \, = \, 10 \, - \, 2\,x \, </math> | ||
| − | + | Lådan som ska byggas är ett rätblock vars volym är höjden <math> \, \times \, </math> basarean: | |
| + | |||
| + | ::<math> V(x) \, = \, x \cdot y^2 \, </math> | ||
Sätter vi in bivillkoret blir problemets målfunktion: | Sätter vi in bivillkoret blir problemets målfunktion: | ||
| Rad 11: | Rad 13: | ||
::<math> \quad V(x) \, = \, x \cdot (10 \, - \, 2\,x)^2 \, </math> | ::<math> \quad V(x) \, = \, x \cdot (10 \, - \, 2\,x)^2 \, </math> | ||
| − | eftersom det är | + | eftersom det är lådans volym som ska maximeras. |
Nuvarande version från 2 februari 2015 kl. 15.09
Från a) har vi problemets bivillkor:
- \[ y \, = \, 10 \, - \, 2\,x \, \]
Lådan som ska byggas är ett rätblock vars volym är höjden \( \, \times \, \) basarean:
- \[ V(x) \, = \, x \cdot y^2 \, \]
Sätter vi in bivillkoret blir problemets målfunktion:
- \[ \quad V(x) \, = \, x \cdot (10 \, - \, 2\,x)^2 \, \]
eftersom det är lådans volym som ska maximeras.