Skillnad mellan versioner av "3.5 Extremvärdesproblem"
Taifun (Diskussion | bidrag) m (→Exempel 1 Glasskiva (rektangel i triangel)) |
Taifun (Diskussion | bidrag) m |
||
| (411 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{Not selected tab|[[3.4 Kurvkonstruktioner|< | + | {{Not selected tab|[[3.4 Kurvkonstruktioner| << Förra avsnitt]]}} |
| − | {{Selected tab|[[3.5 Extremvärdesproblem| | + | {{Selected tab|[[3.5 Extremvärdesproblem|Genomgång]]}} |
{{Not selected tab|[[3.5 Övningar till Extremvärdesproblem|Övningar]]}} | {{Not selected tab|[[3.5 Övningar till Extremvärdesproblem|Övningar]]}} | ||
| − | |||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| + | <!-- | ||
| + | [[Media: Lektion 27 Extremvardesproblem I Ruta.pdf|<strong><span style="color:blue">Lektion 27 Extremvärdesproblem I</span></strong>]] | ||
| − | [[Media: Lektion | + | [[Media: Lektion 28 Extremvardesproblem II Ruta.pdf|<strong><span style="color:blue">Lektion 28 Extremvärdesproblem II</span></strong>]] |
| + | --> | ||
| − | + | <big> | |
| + | <div class="ovnE"><small> | ||
| + | ==== <b><span style="color:#931136">Exempel 1 Rektangel i parabel</span></b> ==== | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td>En rektangel är inbunden i en parabel vars ekvation är given: | ||
| − | + | :::<math> y \, = \, -\,{\, x^2 \over 2} \, + \, 5 \qquad {\rm med} \qquad y \, \geq \, 0 </math> | |
| + | Punkten <math> \, (x,\,y) \, </math> rör sig på parabeln, se figuren. Placera den så | ||
| − | = | + | att rektangelns area <math> \, A \, </math> blir <strong><span style="color:red">maximal</span></strong>. |
| + | |||
| + | |||
| + | '''a)''' Ställ upp rektangelns area som en funktion av <math> \, x \, </math> dvs <math> \, A(x) \, </math>. | ||
| + | |||
| + | '''b)''' Bestäm <math> \, x \, </math> så att <math> \, A(x) \, </math> blir maximal. | ||
| + | |||
| + | '''c)''' Beräkna rektangelns maximala area. | ||
| + | </td> | ||
| + | <td> [[Image: 35 Rektangel i parabel.jpg]] | ||
| + | |||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | '''d)''' Bestäm definitionsmängden till funktionen <math> \, A(x) \, </math> och rita grafen till <math> \, A(x) </math>. Markera maximipunkten från '''b)''' i grafen. | ||
| + | |||
| + | :Kontrollera algebraiskt om maximipunkten ligger inom definitionsmängden. | ||
| + | </small></div> | ||
| + | |||
| + | |||
| + | <div class="ovnE"><small> | ||
| + | '''Lösning:''' | ||
| + | |||
| + | '''a)''' Rektangelns area kan skrivas som <math> \quad A\,(x, \, {\color{Red} y}) \; = \; 2 \, \cdot x \, \cdot \, {\color{Red} y} </math> | ||
| + | |||
| + | :Men <math> \, A\,(x, \, {\color{Red} y}) \, </math> är en funktion av ''två'' variabler som vi inte kan hantera. | ||
| + | |||
| + | :Därför måste <math> A\,(x, \, {\color{Red} y}) \, </math> skrivas om till en funktion <math> \, A\,(x) \, </math> av endast ''en'' variabel, nämligen <math> \, x </math>. | ||
| + | |||
| + | :Detta gör vi genom att eliminera <math> \, {\color{Red} y} \, </math><span style="color:black">:</span> Vi utnyttjar sambandet mellan <math> \, x \, </math> och <math> \, {\color{Red} y} \, </math> som är givet av parabelns ekvation. | ||
| + | |||
| + | :Rektangelns "rörliga" hörn <math> \, (x,\,{\color{Red} y}) \, </math> måste alltid ligga på parabeln. Därför måste <math> \, x \, </math> och <math> \, y \, </math> uppfylla <strong><span style="color:red">parabelns ekvation</span></strong><span style="color:black">:</span> | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td> | + | <td><div style="border:1px solid black; |
| + | display:inline-block !important; | ||
| + | margin-left: 50px !important; | ||
| + | padding:10px 10px 10px 10px; | ||
| + | -webkit-border-radius: 10px;"><strong><math> \displaystyle {\color{Red} y} \, = \, -\,{\, x^2 \over 2} \, + \, 5 </math></strong></div></td> | ||
| + | <td><math> \qquad </math></td> | ||
| + | <td>Detta samband kallas för problemets <strong><span style="color:red">bivillkor</span></strong>.</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | ==== <b><span style="color:#931136">Bivillkor för ett extremvärdesproblem</span></b> ==== | ||
| + | <div class="border-divblue"> | ||
| + | Ett extremvärdesproblems <strong><span style="color:red">bivillkor</span></strong> är ett samband som bestäms av problemets givna geometriska | ||
| + | |||
| + | eller andra föreskrivna egenskaper. | ||
| + | ---- | ||
| + | |||
| + | Bivillkoret sätter ''restriktioner'' (begränsningar, eng. ''constraints'') på punkten <math> (x,\,y)</math>:s rörelsefrihet. | ||
| + | </div> | ||
| + | |||
| + | |||
| + | :I <b><span style="color:#931136">Exempel 1</span></b> är parabelns ekvation problemets bivillkor, därför att punkten <math> (x,\,y) </math> ''måste'' följa parabeln, se figuren ovan. | ||
| + | |||
| + | :Vi använder bivillkoret för att skriva om rektangelns area från en funktion av två variabler <math> \, x \, </math> och <math> \, y \, </math> till en funktion av en variabel <math> \, x </math>. | ||
| + | |||
| + | :Därför sätter vi in parabelns ekvation <math> \, \displaystyle {\color{Red} y} = -\,{\, x^2 \over 2} + 5 \, </math> i rektangelns area <math> \, A\,(x, \, {\color{Red} y}) = 2\cdot x \cdot {\color{Red} y} \, </math> för att eliminera <math> \, {\color{Red} y} \,</math>: | ||
| + | |||
| + | ::::<math> A\,(x, \, {\color{Red} y}) \, = \, 2 \cdot x \cdot {\color{Red} y} \, = \, 2 \cdot x \cdot \left({\color{Red} {-\,{\, x^2 \over 2} \, + \, 5}}\right) \, = \, -\,x^3 \, + \, 10\,x </math> | ||
| + | |||
| + | :På så sätt får vi en funktion för rektangelns area som endast beror av <math> \, x </math>: | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td><div style="border:1px solid black; | ||
| + | display:inline-block !important; | ||
| + | margin-left: 50px !important; | ||
| + | padding:10px 10px 10px 10px; | ||
| + | -webkit-border-radius: 10px;"><strong><math> A\,(x) \, = \, \displaystyle -\,x^3 \, + \, 10\,x </math></strong></div></td> | ||
| + | <td><math> \qquad </math></td> | ||
| + | <td>Denna funktion kallas för problemets <strong><span style="color:red">målfunktion</span></strong></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | |||
| + | ==== <b><span style="color:#931136">Målfunktion för ett extremvärdesproblem</span></b> ==== | ||
| + | <div class="border-divblue"> | ||
| + | Ett extremvärdesproblems <strong><span style="color:red">målfunktion</span></strong> är alltid den funktion av endast ''en'' variabel som ska | ||
| + | |||
| + | maximeras eller minimeras. | ||
| + | ---- | ||
| + | |||
| + | Extremvärdesproblem består i regel av ett bivillkor och en målfunktion. | ||
| + | ---- | ||
| + | |||
| + | Bivillkoret används för att reducera målfunktionen till en funktion av endast ''en'' variabel. | ||
| + | </div> | ||
| + | |||
| + | |||
| + | :I <b><span style="color:#931136">Exempel 1</span></b> är <math> A\,(x) </math> problemets målfunktion, därför att det är rektangelns area som ska maximeras. | ||
| + | |||
| + | I <math> A\,(x) </math> är parabelns ekvation redan "inbakad". | ||
| + | |||
| + | ---- | ||
| + | |||
| + | |||
| + | '''b)''' För att hitta målfunktionens lokala maximum deriverar vi <math> \, A(x) \, </math> och bestämmer derivatans nollställen: | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td> | ||
| + | ::<math> A(x) \, = \, -\,x^3 \, + \, 10\,x </math> | ||
| + | |||
| + | ::<math> A'(x) \, = \, -\,3\,x^2 \, + \, 10 </math> | ||
| + | |||
| + | ::<math> A''(x) \, = \, -\,6\,x </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</td> | </td> | ||
| − | <td>& | + | <td><math> \qquad </math></td> |
| + | <td>Derivatans nollställen: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><math> \qquad </math></td> | ||
| + | <td><math>\begin{array}{rcrcl} A'(x) & = & -3\,x^2 \, + \, 10 & = & 0 \\ | ||
| + | & & 10 & = & 3\,x^2 \\ | ||
| + | & & {10 \over 3} & = & x^2 \\ | ||
| + | & & x_{1, 2} & = & \sqrt{10 \over 3} \\ | ||
| + | & & x_1 & = & 1,83 \\ | ||
| + | & & x_2 & = & -1,83 | ||
| + | \end{array}</math> | ||
| + | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | ''' | + | <math> \quad\; x_2 = -1,83 \, </math> förkastas därför att arean och därmed <math> \, x \, </math> inte kan vara negativ, se även '''d)'''. |
| − | + | :Vi sätter in <math> \, x_1 = 1,83 \, </math> i andraderivatan och använder [[3.2_Lokala_maxima_och_minima#Regler_om_max.2Fmin_med_andraderivatan|<strong><span style="color:blue">reglerna om max/min</span></strong>]]<span style="color:black">:</span> | |
| − | + | <math> \qquad\quad A''(1,83) = -6 \cdot 1,83 \, < \, 0 \quad \Longrightarrow \quad A(x) \, </math> har ett lokalt maximum i <math> \; \boxed{x \, = \, 1,83} \, </math>. | |
| − | + | :För <math> \, x = 1,83 \, {\rm cm} \, </math> antar målfunktionen (rektangelns area) sitt maximum. | |
| + | ---- | ||
| + | |||
| + | '''c)''' För att bestämma rektangelns maximala area sätter vi in <math> \, x = 1,83 \, </math> i målfunktionen <math> \, A(x) </math>: | ||
| + | |||
| + | :::<math> A\,(x) \, = \, \displaystyle -\,x^3 \, + \, 10\,x </math> | ||
| + | |||
| + | :::<math> A(1,83) = -\,1,83\,^3 \, + \, 10 \cdot 1,83 \, = \, 12,17 </math> | ||
| + | |||
| + | :Rektangelns maximala area är <math> \, 12,17 \, </math>. | ||
| + | ---- | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | + | <td> | |
| + | '''d)''' Målfunktionen <math> \, A\,(x) = \displaystyle -\,x^3 \, + \, 10\,x \, </math> har definitionsintervallet<span style="color:black">: | ||
| − | Triangelns hypotenusa blir då en del av en rät linje. | + | </span> <div style="border:1px solid black; |
| + | display:inline-block !important; | ||
| + | margin-left: 150px !important; | ||
| + | padding:10px 10px 10px 10px; | ||
| + | -webkit-border-radius: 10px;"><strong><math> \, 0 \, \leq \, x \, \leq \, \sqrt{10} </math></strong></div> | ||
| + | |||
| + | :Den vänstra ändan <math> \, 0 \, </math> är motiverad av att arean och därmed <math> \, x \, </math> inte kan vara negativ. | ||
| + | |||
| + | :Den högra ändan <math> \, \sqrt{10} \, </math> är parabelns högra rand i [[3.5_Extremvärdesproblem#Exempel_1_Rektangel_i_parabel|<b><span style="color:blue">Exempel 1</span></b>]], dvs den positiva lös- | ||
| + | |||
| + | :ningen till ekvationen <math> \displaystyle -{x^2 \over 2} + 5 = 0 </math>. För <math> x > \sqrt{10} </math> blir <math> y < 0 </math>, vilket inte är tillåtet. | ||
| + | |||
| + | :Maximipunkten <math> \, x = 1,83 \, </math> ligger inom definitionsmängden<span style="color:black">:</span> <math> \, 0 \, < \, 1,83 \, < \, \sqrt{10} </math>. | ||
| + | </td> | ||
| + | <td> [[Image: Ex_1_Malfunktion.jpg]]</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | </small></div> | ||
| + | |||
| + | |||
| + | <div class="ovnC"><small> | ||
| + | ==== <b><span style="color:#931136">Exempel 2 Glasskiva (rektangel i triangel)</span></b> ==== | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td>En glasskiva har formen av en rätvinklig triangel med följande mått<span style="color:black">:</span> | ||
| + | |||
| + | <math> \qquad\qquad\qquad\quad </math> Kortare kateten <math> \, = \, 20 \, </math> cm | ||
| + | |||
| + | <math> \qquad\qquad\qquad\quad </math> Längre kateten <math> \, = \, 30 \, </math> cm | ||
| + | |||
| + | En <b><span style="color:red">rektangulär glasplatta med maximal area</span></b> ska skäras ut ur skivan. | ||
| + | |||
| + | '''a)''' Formulera problemets bivillkor. | ||
| + | |||
| + | '''b)''' Ställ upp problemets målfunktion. Ange dess definitionsmängd. | ||
| + | </td> | ||
| + | <td> [[Image: Ovn 3_2_10_40.jpg]]</td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | '''c)''' Bestäm <math> \, x \, </math> så att glasplattans area <math> \, A(x) \, </math> maximeras. | ||
| + | |||
| + | '''d)''' Beräkna glasplattans maximala area. | ||
| + | </small></div> | ||
| + | |||
| + | |||
| + | <div class="ovnC"><small> | ||
| + | '''Lösning:''' | ||
| + | |||
| + | '''a)''' Vi inför beteckningen <math> \; {\color{Red} y} \; </math> för glasplattans andra sida, så att rektangelns area kan skrivas som <math> \; A\,(x, {\color{Red} y}) \; = \; x \; \cdot \; {\color{Red} y} </math> | ||
| + | |||
| + | För att skriva om funktionen ovan till en funktion <math> \, A\,(x) \, </math> av endast ''en'' variabel, nämligen <math> \, x \, </math>, | ||
| + | |||
| + | måste <math> \, {\color{Red} y} \, </math> uttryckas med <math> \, x \, </math>, så att <math> \, {\color{Red} y} \, </math> kan elimineras. | ||
| + | |||
| + | Sambandet mellan <math> \, x \, </math> och <math> \, {\color{Red} y} \, </math> bestäms av rektangelns "rörliga" hörn som är bundet till triangelns hypotenusa. | ||
| + | |||
| + | Vi inför ett koordinatsystem och sätter glasskivan i det, se bilden: | ||
| + | |||
| + | <table> | ||
| + | <tr> | ||
| + | <td>Triangelns hypotenusa blir då en del av en rät linje. | ||
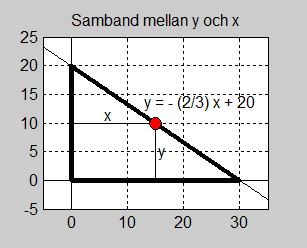
Punkten <math> \, (x, y) \, </math> rör sig på denna räta linje vars ekvation är: | Punkten <math> \, (x, y) \, </math> rör sig på denna räta linje vars ekvation är: | ||
| Rad 58: | Rad 258: | ||
Skärningspunkten med <math>\,y</math>-axeln<span style="color:black">:</span> <math> \quad m \, = \, 20 </math> | Skärningspunkten med <math>\,y</math>-axeln<span style="color:black">:</span> <math> \quad m \, = \, 20 </math> | ||
| − | Den räta linjens ekvation blir då<span style="color:black">:</span> <div style="border:1px solid black; | + | Den räta linjens ekvation blir då problemets bivillkor<span style="color:black">:</span> |
| + | |||
| + | :::<div style="border:1px solid black; | ||
display:inline-block !important; | display:inline-block !important; | ||
| − | margin-left: | + | margin-left: 52px !important; |
padding:10px 10px 10px 10px; | padding:10px 10px 10px 10px; | ||
-webkit-border-radius: 10px;"><strong><math> \displaystyle {\color{Red} y} \, = \, - \, {2 \over 3}\,x \, + \, 20 </math></strong></div> | -webkit-border-radius: 10px;"><strong><math> \displaystyle {\color{Red} y} \, = \, - \, {2 \over 3}\,x \, + \, 20 </math></strong></div> | ||
| − | |||
</td> | </td> | ||
| − | <td> [[Image: Ovn 3_2_10a.jpg]]</td> | + | <td> [[Image: Ovn 3_2_10a.jpg]] |
| + | |||
| + | |||
| + | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | |||
| − | + | '''b)''' Det ovan formulerade bivillkoret för glasskivan sätts in i <math> \; A\,(x, {\color{Red} y}) = x \cdot {\color{Red} y} \; </math> för att eliminera <math> \, {\color{Red} y} \,</math> | |
| − | + | och ställa upp ett uttryck för arean som endast beror av <math> \, x </math>: | |
| − | + | ::<math> A\,(x, \, {\color{Red} y}) \, = \, x \cdot {\color{Red} y} \, = \, x \cdot \left(-\,{2 \over 3}\,x \, + \, 20\right) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x </math> | |
| − | <div style="border:1px solid black; | + | Målfunktionen är<span style="color:black">:</span> <div style="border:1px solid black; |
display:inline-block !important; | display:inline-block !important; | ||
| − | margin-left: | + | margin-left: 25px !important; |
padding:10px 10px 10px 10px; | padding:10px 10px 10px 10px; | ||
| − | -webkit-border-radius: 10px;"><strong><math> A\,(x) \, = \, \displaystyle -\,{2 \over 3}\,x^2 \, + \, 20\,x </math></strong></div> | + | -webkit-border-radius: 10px;"><strong><math> A\,(x) \, = \, \displaystyle -\,{2 \over 3}\,x^2 \, + \, 20\,x </math></strong></div> med definitionsmängden<span style="color:black">:</span> <math> \quad 0 \, \leq \, x \, \leq \, 30 \,</math>. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''c)''' För att hitta målfunktionens lokala maximum deriverar vi <math> \, A(x) \, </math> och bestämmer derivatans nollställen: | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td> | ||
::<math> A(x) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x </math> | ::<math> A(x) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x </math> | ||
| Rad 96: | Rad 297: | ||
::<math> A''(x) \, = \, -\,{4 \over 3} </math> | ::<math> A''(x) \, = \, -\,{4 \over 3} </math> | ||
| + | </td> | ||
| + | <td><math> \qquad </math></td> | ||
| + | <td>Derivatans nollställen: | ||
| − | |||
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><math> \qquad </math></td> | ||
| + | <td><math>\begin{array}{rcrcl} A'(x) & = & -{4 \over 3}\,x + 20 & = & 0 \\ | ||
& & 20 & = & {4 \over 3}\,x \\ | & & 20 & = & {4 \over 3}\,x \\ | ||
| − | & & {20 \cdot 3 \over 4} & = & x \\ | + | & & {20 \, \cdot \, 3 \over 4} & = & x \\ |
& & x & = & 15 | & & x & = & 15 | ||
\end{array}</math> | \end{array}</math> | ||
| − | |||
| − | + | </td> | |
| + | </tr> | ||
| + | </table> | ||
| − | + | <math> \, x = 15 \, </math> som ligger inom målfunktionens definitionsmängd, sätts in i andraderivatan enligt [[3.2_Lokala_maxima_och_minima#Regler_om_max.2Fmin_med_andraderivatan|<strong><span style="color:blue">reglerna om max/min</span></strong>]]<span style="color:black">:</span> | |
| − | + | <math> A''(15) = \displaystyle -\,{4 \over 3} \,<\, 0 \quad \Longrightarrow \quad A(x) \, </math> har ett lokalt maximum i <math> \; \boxed{x \, = \, 15} \, </math>. | |
| − | + | ||
| + | För <math> \, x = 15 \, {\rm cm} \, </math> antar målfunktionen ett maximum, dvs rektangelns area blir maximal. | ||
| − | + | ||
| + | '''d)''' Eftersom rektangeln får sin största area för <math> \, x = 15 \, </math> sätter vi in <math> \, x = 15 \, </math> i målfunktionen för att få största arean: | ||
| + | |||
| + | ::<math> A\,(x) \, = \, \displaystyle -\,{2 \over 3}\,x^2 \, + \, 20\,x </math> | ||
::<math> A(15) = -\,{2 \over 3} \cdot 15^2 + 20 \cdot 15 = 150 </math> | ::<math> A(15) = -\,{2 \over 3} \cdot 15^2 + 20 \cdot 15 = 150 </math> | ||
Glasplattans största area blir <math> \, 150 \, {\rm cm}^2 \, </math>. | Glasplattans största area blir <math> \, 150 \, {\rm cm}^2 \, </math>. | ||
| + | </small></div> | ||
| − | |||
| + | <div class="ovnA"><small> | ||
| + | ==== <b><span style="color:#931136">Exempel 3 Konservburk</span></b> ==== | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td>En | + | <td>En cylinderformad konservburk ska produceras av en bit plåt. Vi antar: |
| − | + | Plåtens area <math> \, = \, </math> cylinderns begränsnings<b><span style="color:red">area</span></b> <math> \, {\color{Red} {= \, 500 \, {\rm cm}^2}} \, </math> efter spill. | |
| − | + | Vilka mått på cylindern måste väljas så att <b><span style="color:red">volymen</span></b> blir <b><span style="color:red">maximal</span></b> ? | |
| − | |||
| − | + | '''a)''' Formulera problemets bivillkor. | |
| − | + | '''b)''' Ställ upp problemets målfunktion. | |
| − | + | '''c)''' Bestäm cylinderns radie och höjd så att burkens volym | |
| + | :blir maximal.</td> | ||
| + | <td> </td> | ||
| + | <td>[[Image: Konservburk_40a.jpg]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | '''d)''' Ange målfunktionens definitionsmängd. Rita graferna till bivillkoret och målfunktionen. Tolka graferna. | ||
| + | '''e)''' Beräkna konservburkens maximala volym. | ||
| + | |||
| + | '''f)''' Vilket samband råder mellan cylinderns radie <math> \, r \, </math> och dess höjd <math> \, h \, </math> när volymen maximeras? | ||
| + | </small></div> | ||
| + | |||
| + | |||
| + | <div class="ovnA"><small> | ||
'''Lösning:''' | '''Lösning:''' | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td>'''a)''' Begränsningsarean <math> \, A \, = \, 2\,\pi\,r\,h \, + 2\,\pi\,r^2 \, = \, 500 </math> | ||
| − | + | ::<math>\begin{array}{rcl} 2\,\pi\,r\,h \, + 2\,\pi\,r^2 & = & 500 \\ | |
| + | 2\,\pi\,r\,h & = & 500 \, - 2\,\pi\,r^2 \\ | ||
| + | h & = & {500 - 2\,\pi\,r^2 \over 2\,\pi\,r} \\ | ||
| + | h & = & {500 \over 2\,\pi\,r} \, - \, r \, = \, {250 \over \pi\,r} \, - \, r | ||
| + | \end{array}</math> | ||
| + | Därmed är bivillkoret: <div style="border:1px solid black; | ||
| + | display:inline-block !important; | ||
| + | margin-left: 25px !important; | ||
| + | padding:10px 10px 10px 10px; | ||
| + | -webkit-border-radius: 10px;"><strong><math> h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r </math></strong></div> | ||
</td> | </td> | ||
| − | <td> | + | <td> </td> |
| − | <td>[[Image: | + | <td>[[Image: Zylinder01.gif]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | |||
| − | + | '''b)''' Cylinderns volym <math> \, V \, </math> är basytan <math> \times </math> höjden dvs<span style="color:black">:</span> <math> \qquad V\,(r, \, {\color{Red} h}) \; = \; \pi \, r^2 \; \cdot \; {\color{Red} h} \qquad </math> Funktion av två variabler<span style="color:black">:</span> <math> \, r \, </math> och <math> \, {\color{Red} h} \, </math>. | |
| + | |||
| + | |||
| + | För att skriva om denna funktion till en funktion av endast en variabel, sätter vi in bivillkoret från '''a)''' i <math> \, V\,(r, \, {\color{Red} h}) \, </math> och eliminerar <math> \, {\color{Red} h} \, </math><span style="color:black">:</span> | ||
| + | |||
| + | :::<math> V\,(r, \, {\color{Red} h}) \, = \, \pi \, r^2 \; \cdot \; {\color{Red} h} \, = \, \pi\,r^2\cdot \left( {\color{Red} {{250 \over \pi\,r}\,-\, r}} \right) \, = \, {250 \cdot \pi\,r^2 \over \pi\,r} \, - \, \pi\,r^3 \, = \, 250 \cdot r \, - \, \pi\,r^3 </math> | ||
| + | |||
| + | Därmed blir målfunktionen: <div style="border:1px solid black; | ||
| + | display:inline-block !important; | ||
| + | margin-left: 25px !important; | ||
| + | padding:10px 10px 10px 10px; | ||
| + | -webkit-border-radius: 10px;"><strong><math> V(r) \, = \, 250 \, r \, - \, \pi\,r^3 </math></strong></div> | ||
| + | |||
| + | |||
| + | '''c)''' Målfunktionen maximeras: | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td> | ||
| + | ::<math> V(r) \, = \, 250 \, r \, - \, \pi\,r^3 </math> | ||
| + | |||
| + | ::<math> V'(r) \, = \, 250 \, - \, 3\,\pi\,r^2 </math> | ||
| + | |||
| + | ::<math> V''(r) \, = \, -\,6\,\pi\,r </math> | ||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><math> \qquad </math></td> | ||
| + | <td>Derivatans nollställen: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | </td> | ||
| + | <td><math> \qquad </math></td> | ||
| + | <td><math>\begin{array}{rcrcl} V'(r) & = & 250 \, - \, 3\,\pi\,r^2 & = & 0 \\ | ||
| + | & & 250 & = & 3\,\pi\,r^2 \\ | ||
| + | & & {250 \over 3\,\pi} & = & r^2 \\ | ||
| + | & & r_{1, 2} & = & \pm\,\sqrt{250 \over 3\,\pi} \\ | ||
| + | & & r & = & 5,15 | ||
| + | \end{array}</math> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <math> r_2 = -5,15 \, </math> förkastas, för radien kan inte bli negativ. <math> \, r = 5,15 \, > \, 0 \, </math> sätts in i andraderivatan enligt [[3.2_Lokala_maxima_och_minima#Regler_om_max.2Fmin_med_andraderivatan|<strong><span style="color:blue">reglerna om max/min</span></strong>]]<span style="color:black">:</span> | ||
| + | |||
| + | <math> V''(5,15) = -6 \,\pi\cdot 5,15 \, < \, 0 \quad \Longrightarrow \quad V(r) \, </math> har ett lokalt maximum för <math> \, r = 5,15 </math>. | ||
| + | |||
| + | För att få cylinderns höjd när volymen maximeras sätter vi in <math> \, r = 5,15 \, </math> i bivillkoret från '''a)'''<span style="color:black">:</span> | ||
| + | |||
| + | :::::<math> h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \, = \, {250 \over \pi\cdot 5,15} \, - \, 5,15 \, = \, 10,30 </math> | ||
| + | |||
| + | Cylinderns volym blir maximal för radien <math> \quad \boxed{r = 5,15 \; {\rm cm}} \quad </math> och höjden <math> \quad \boxed{h = 10,30 \; {\rm cm}} \quad </math>. | ||
| + | |||
| + | |||
| + | '''d)''' För att bestämma målfunktionens definitionsmängd tittar undersöker vi bivillkoret<span style="color:black">:</span> <math> \qquad h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r </math> | ||
| + | |||
| + | Av detta framgår att <math> \, r \, </math> inte får vara <math> \, 0 \, </math><span style="color:black">:</span> <math> \; r \, \neq \, 0 \; </math>. Därför är <math> \, 0 \, </math> en undre gräns för <math> \, r </math><span style="color:black">:</span> <math> \qquad r \, > \, 0 </math> | ||
| + | |||
| + | För att hitta en övre gräns (största möjliga värde) för <math> \; r \; </math> tittar vi på cylinderns begränsningsarea<span style="color:black">:</span> | ||
| + | |||
| + | :::::<math> \, A \, = \, 2\,\pi\,r\,h \, + 2\,\pi\,r^2 \, = \, 500 </math> | ||
| + | |||
| + | Pga begränsningsareans konstanta värde <math> \, 500 \, </math> blir cylinderns radie störst när höjden blir <math> \, 0 \, </math>. | ||
| + | |||
| + | Därför får vi radiens störst möjliga värde om vi i formeln ovan väljer <math> \, h=0 </math><span style="color:black">:</span> | ||
| + | |||
| + | :::::<math> \, h = 0 \qquad \Longrightarrow \qquad A \, = \, 2\,\pi \cdot \left(r\right)\,^2 \, = \, 500 \qquad \Longrightarrow \qquad r \, = \, \sqrt{500 \over 2\,\pi} \, = \, 8,92 </math> | ||
| + | |||
| + | Därmed blir målfunktionens definitionsmängd<span style="color:black">:</span><math> \qquad\qquad </math><div style="border:1px solid black; | ||
| + | display:inline-block !important; | ||
| + | margin-left: 25px !important; | ||
| + | padding:10px 10px 10px 10px; | ||
| + | -webkit-border-radius: 10px;"><strong><math> 0 \; < \; r \; \leq \; 8,92 </math></strong></div> | ||
| + | |||
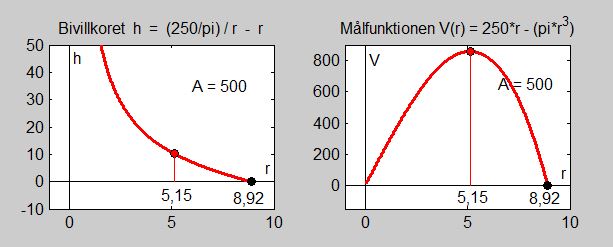
| + | Grafen till vänster visar bivillkoret <math> h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r </math> och till höger målfunktionen <math> V(r) \, = \, 250 \, r \, - \, \pi\,r^3 </math>, båda med definitionsmängden ovan. | ||
| + | |||
| + | :[[Image: Konservburk Grafer.jpg]] | ||
| + | |||
| + | Målfunktionens graf till höger bekräftar det algebraiska resultatet från '''c)''', nämligen att volymen blir maximal för <math> \, r = 5,15 </math>. | ||
| + | |||
| + | Bivillkorets graf till vänster bekräftar att för <math> \, r = 5,15 \, </math> höjden blir <math> \, \approx \, 10 </math> och dessutom att <math> \, r \, </math> inte kan bli större än <math> \, 8,92 </math>. | ||
| + | |||
| + | |||
| + | '''e)''' Resultaten från '''c)''' sätts in i målfunktionen för att få cylinderns största volym<span style="color:black">:</span> | ||
| + | |||
| + | ::<math> V(5,15) \, = \, \pi \, \cdot 5,15^2 \, \cdot 10,30 \, = \, 858,23 </math> | ||
| + | |||
| + | Konservburkens maximala volym blir <math> \; 858,23 \, {\rm cm}^3 \; </math>. | ||
| + | |||
| + | |||
| + | '''f)''' Följande samband råder mellan cylinderns radie <math> \; r = 5,15 \, {\rm cm} \; </math> och dess höjd <math> \; h = 10,30 \, {\rm cm}</math> | ||
| + | |||
| + | när volymen till en cylinder med en begränsningsarea på <math> \, 500 \, {\rm cm}^2 \, </math>, maximeras<span style="color:black">:</span> | ||
| + | |||
| + | ::::<div style="border:1px solid black; | ||
| + | display:inline-block !important; | ||
| + | margin-left: 25px !important; | ||
| + | padding:10px 10px 10px 10px; | ||
| + | -webkit-border-radius: 10px;"><strong><math> 2 \; r \; = \; h </math></strong></div> | ||
| + | </small></div> | ||
| + | |||
| + | |||
| + | Återstår frågan som är föremål för undersökning i [[3.5_Övningar_till_Extremvärdesproblem#.C3.96vning_9|<strong><span style="color:blue">övning 9</span></strong>]], om samma samband även råder <strong><span style="color:red">generellt</span></strong> mellan radien <math> \; r \; </math> och höjden <math> \; h \; </math> för alla konservburkar med vilken begränsningsarea som helst och maximal volym, nämligen<span style="color:black">:</span> | ||
| + | |||
| + | ::<div style="border:1px solid black; | ||
| + | display:inline-block !important; | ||
| + | margin-left: 70px !important; | ||
| + | padding:10px 10px 10px 10px; | ||
| + | -webkit-border-radius: 10px;"><strong> Diametern <math> \; = \; </math> Höjden </strong></div> | ||
| + | |||
| + | En annan intressant frågeställning är: | ||
| + | |||
| + | Råder även sambandet ovan om man utgår från en konservburk med fast given volym vars materialåtgång ska minimeras? | ||
| + | |||
| + | En närmare undersökning liknande lösningen till [[3.5_Extremvärdesproblem#Exempel_3_Konservburk|<strong><span style="color:blue">Exempel 3</span></strong>]] kommer att visa att detta är fallet. | ||
| + | |||
| + | Dvs sambandet ovan är alltid optimalt ur ekonomisk synpunkt. | ||
| + | |||
| + | |||
| + | == <b><span style="color:#931136">Ett ekonomiskt exempel</span></b> == | ||
| + | |||
| + | |||
| + | Se [[3.5_Övningar_till_Extremvärdesproblem#.C3.96vning_7|<strong><span style="color:blue">övning 7</span></strong>]]. | ||
| + | </big> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | : | + | [[Matte:Copyrights|Copyright]] © 2011-2016 Math Online Sweden AB. All Rights Reserved. |
Nuvarande version från 13 juni 2020 kl. 16.57
| << Förra avsnitt | Genomgång | Övningar |
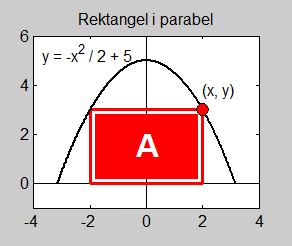
Exempel 1 Rektangel i parabel
d) Bestäm definitionsmängden till funktionen \( \, A(x) \, \) och rita grafen till \( \, A(x) \). Markera maximipunkten från b) i grafen.
- Kontrollera algebraiskt om maximipunkten ligger inom definitionsmängden.
Lösning:
a) Rektangelns area kan skrivas som \( \quad A\,(x, \, {\color{Red} y}) \; = \; 2 \, \cdot x \, \cdot \, {\color{Red} y} \)
- Men \( \, A\,(x, \, {\color{Red} y}) \, \) är en funktion av två variabler som vi inte kan hantera.
- Därför måste \( A\,(x, \, {\color{Red} y}) \, \) skrivas om till en funktion \( \, A\,(x) \, \) av endast en variabel, nämligen \( \, x \).
- Detta gör vi genom att eliminera \( \, {\color{Red} y} \, \): Vi utnyttjar sambandet mellan \( \, x \, \) och \( \, {\color{Red} y} \, \) som är givet av parabelns ekvation.
- Rektangelns "rörliga" hörn \( \, (x,\,{\color{Red} y}) \, \) måste alltid ligga på parabeln. Därför måste \( \, x \, \) och \( \, y \, \) uppfylla parabelns ekvation:
\( \displaystyle {\color{Red} y} \, = \, -\,{\, x^2 \over 2} \, + \, 5 \) |
\( \qquad \) | Detta samband kallas för problemets bivillkor. |
Bivillkor för ett extremvärdesproblem
Ett extremvärdesproblems bivillkor är ett samband som bestäms av problemets givna geometriska
eller andra föreskrivna egenskaper.
Bivillkoret sätter restriktioner (begränsningar, eng. constraints) på punkten \( (x,\,y)\):s rörelsefrihet.
- I Exempel 1 är parabelns ekvation problemets bivillkor, därför att punkten \( (x,\,y) \) måste följa parabeln, se figuren ovan.
- Vi använder bivillkoret för att skriva om rektangelns area från en funktion av två variabler \( \, x \, \) och \( \, y \, \) till en funktion av en variabel \( \, x \).
- Därför sätter vi in parabelns ekvation \( \, \displaystyle {\color{Red} y} = -\,{\, x^2 \over 2} + 5 \, \) i rektangelns area \( \, A\,(x, \, {\color{Red} y}) = 2\cdot x \cdot {\color{Red} y} \, \) för att eliminera \( \, {\color{Red} y} \,\):
- \[ A\,(x, \, {\color{Red} y}) \, = \, 2 \cdot x \cdot {\color{Red} y} \, = \, 2 \cdot x \cdot \left({\color{Red} {-\,{\, x^2 \over 2} \, + \, 5}}\right) \, = \, -\,x^3 \, + \, 10\,x \]
- På så sätt får vi en funktion för rektangelns area som endast beror av \( \, x \):
\( A\,(x) \, = \, \displaystyle -\,x^3 \, + \, 10\,x \) |
\( \qquad \) | Denna funktion kallas för problemets målfunktion |
Målfunktion för ett extremvärdesproblem
Ett extremvärdesproblems målfunktion är alltid den funktion av endast en variabel som ska
maximeras eller minimeras.
Extremvärdesproblem består i regel av ett bivillkor och en målfunktion.
Bivillkoret används för att reducera målfunktionen till en funktion av endast en variabel.
- I Exempel 1 är \( A\,(x) \) problemets målfunktion, därför att det är rektangelns area som ska maximeras.
I \( A\,(x) \) är parabelns ekvation redan "inbakad".
b) För att hitta målfunktionens lokala maximum deriverar vi \( \, A(x) \, \) och bestämmer derivatans nollställen:
|
\( \qquad \) | Derivatans nollställen:
|
\( \qquad \) | \(\begin{array}{rcrcl} A'(x) & = & -3\,x^2 \, + \, 10 & = & 0 \\ & & 10 & = & 3\,x^2 \\ & & {10 \over 3} & = & x^2 \\ & & x_{1, 2} & = & \sqrt{10 \over 3} \\ & & x_1 & = & 1,83 \\ & & x_2 & = & -1,83 \end{array}\) |
\( \quad\; x_2 = -1,83 \, \) förkastas därför att arean och därmed \( \, x \, \) inte kan vara negativ, se även d).
- Vi sätter in \( \, x_1 = 1,83 \, \) i andraderivatan och använder reglerna om max/min:
\( \qquad\quad A''(1,83) = -6 \cdot 1,83 \, < \, 0 \quad \Longrightarrow \quad A(x) \, \) har ett lokalt maximum i \( \; \boxed{x \, = \, 1,83} \, \).
- För \( \, x = 1,83 \, {\rm cm} \, \) antar målfunktionen (rektangelns area) sitt maximum.
c) För att bestämma rektangelns maximala area sätter vi in \( \, x = 1,83 \, \) i målfunktionen \( \, A(x) \):
- \[ A\,(x) \, = \, \displaystyle -\,x^3 \, + \, 10\,x \]
- \[ A(1,83) = -\,1,83\,^3 \, + \, 10 \cdot 1,83 \, = \, 12,17 \]
- Rektangelns maximala area är \( \, 12,17 \, \).
|
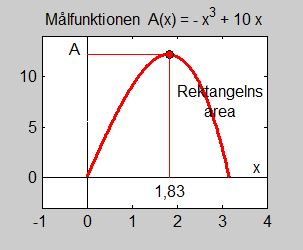
d) Målfunktionen \( \, A\,(x) = \displaystyle -\,x^3 \, + \, 10\,x \, \) har definitionsintervallet: \( \, 0 \, \leq \, x \, \leq \, \sqrt{10} \)
|
 |
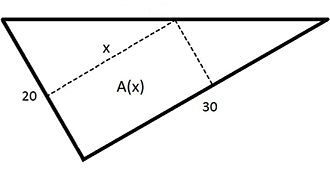
Exempel 2 Glasskiva (rektangel i triangel)
c) Bestäm \( \, x \, \) så att glasplattans area \( \, A(x) \, \) maximeras.
d) Beräkna glasplattans maximala area.
Lösning:
a) Vi inför beteckningen \( \; {\color{Red} y} \; \) för glasplattans andra sida, så att rektangelns area kan skrivas som \( \; A\,(x, {\color{Red} y}) \; = \; x \; \cdot \; {\color{Red} y} \)
För att skriva om funktionen ovan till en funktion \( \, A\,(x) \, \) av endast en variabel, nämligen \( \, x \, \),
måste \( \, {\color{Red} y} \, \) uttryckas med \( \, x \, \), så att \( \, {\color{Red} y} \, \) kan elimineras.
Sambandet mellan \( \, x \, \) och \( \, {\color{Red} y} \, \) bestäms av rektangelns "rörliga" hörn som är bundet till triangelns hypotenusa.
Vi inför ett koordinatsystem och sätter glasskivan i det, se bilden:
b) Det ovan formulerade bivillkoret för glasskivan sätts in i \( \; A\,(x, {\color{Red} y}) = x \cdot {\color{Red} y} \; \) för att eliminera \( \, {\color{Red} y} \,\)
och ställa upp ett uttryck för arean som endast beror av \( \, x \):
- \[ A\,(x, \, {\color{Red} y}) \, = \, x \cdot {\color{Red} y} \, = \, x \cdot \left(-\,{2 \over 3}\,x \, + \, 20\right) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x \]
c) För att hitta målfunktionens lokala maximum deriverar vi \( \, A(x) \, \) och bestämmer derivatans nollställen:
|
\( \qquad \) | Derivatans nollställen:
|
\( \qquad \) | \(\begin{array}{rcrcl} A'(x) & = & -{4 \over 3}\,x + 20 & = & 0 \\
& & 20 & = & {4 \over 3}\,x \\
& & {20 \, \cdot \, 3 \over 4} & = & x \\
& & x & = & 15
\end{array}\)
|
\( \, x = 15 \, \) som ligger inom målfunktionens definitionsmängd, sätts in i andraderivatan enligt reglerna om max/min:
\( A''(15) = \displaystyle -\,{4 \over 3} \,<\, 0 \quad \Longrightarrow \quad A(x) \, \) har ett lokalt maximum i \( \; \boxed{x \, = \, 15} \, \).
För \( \, x = 15 \, {\rm cm} \, \) antar målfunktionen ett maximum, dvs rektangelns area blir maximal.
d) Eftersom rektangeln får sin största area för \( \, x = 15 \, \) sätter vi in \( \, x = 15 \, \) i målfunktionen för att få största arean:
- \[ A\,(x) \, = \, \displaystyle -\,{2 \over 3}\,x^2 \, + \, 20\,x \]
- \[ A(15) = -\,{2 \over 3} \cdot 15^2 + 20 \cdot 15 = 150 \]
Glasplattans största area blir \( \, 150 \, {\rm cm}^2 \, \).
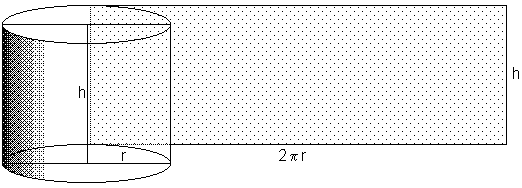
Exempel 3 Konservburk
d) Ange målfunktionens definitionsmängd. Rita graferna till bivillkoret och målfunktionen. Tolka graferna.
e) Beräkna konservburkens maximala volym.
f) Vilket samband råder mellan cylinderns radie \( \, r \, \) och dess höjd \( \, h \, \) när volymen maximeras?
Lösning:
b) Cylinderns volym \( \, V \, \) är basytan \( \times \) höjden dvs: \( \qquad V\,(r, \, {\color{Red} h}) \; = \; \pi \, r^2 \; \cdot \; {\color{Red} h} \qquad \) Funktion av två variabler: \( \, r \, \) och \( \, {\color{Red} h} \, \).
För att skriva om denna funktion till en funktion av endast en variabel, sätter vi in bivillkoret från a) i \( \, V\,(r, \, {\color{Red} h}) \, \) och eliminerar \( \, {\color{Red} h} \, \):
- \[ V\,(r, \, {\color{Red} h}) \, = \, \pi \, r^2 \; \cdot \; {\color{Red} h} \, = \, \pi\,r^2\cdot \left( {\color{Red} {{250 \over \pi\,r}\,-\, r}} \right) \, = \, {250 \cdot \pi\,r^2 \over \pi\,r} \, - \, \pi\,r^3 \, = \, 250 \cdot r \, - \, \pi\,r^3 \]
c) Målfunktionen maximeras:
|
\( \qquad \) | Derivatans nollställen:
|
\( \qquad \) | \(\begin{array}{rcrcl} V'(r) & = & 250 \, - \, 3\,\pi\,r^2 & = & 0 \\ & & 250 & = & 3\,\pi\,r^2 \\ & & {250 \over 3\,\pi} & = & r^2 \\ & & r_{1, 2} & = & \pm\,\sqrt{250 \over 3\,\pi} \\ & & r & = & 5,15 \end{array}\) |
\( r_2 = -5,15 \, \) förkastas, för radien kan inte bli negativ. \( \, r = 5,15 \, > \, 0 \, \) sätts in i andraderivatan enligt reglerna om max/min:
\( V''(5,15) = -6 \,\pi\cdot 5,15 \, < \, 0 \quad \Longrightarrow \quad V(r) \, \) har ett lokalt maximum för \( \, r = 5,15 \).
För att få cylinderns höjd när volymen maximeras sätter vi in \( \, r = 5,15 \, \) i bivillkoret från a):
- \[ h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \, = \, {250 \over \pi\cdot 5,15} \, - \, 5,15 \, = \, 10,30 \]
Cylinderns volym blir maximal för radien \( \quad \boxed{r = 5,15 \; {\rm cm}} \quad \) och höjden \( \quad \boxed{h = 10,30 \; {\rm cm}} \quad \).
d) För att bestämma målfunktionens definitionsmängd tittar undersöker vi bivillkoret: \( \qquad h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \)
Av detta framgår att \( \, r \, \) inte får vara \( \, 0 \, \): \( \; r \, \neq \, 0 \; \). Därför är \( \, 0 \, \) en undre gräns för \( \, r \): \( \qquad r \, > \, 0 \)
För att hitta en övre gräns (största möjliga värde) för \( \; r \; \) tittar vi på cylinderns begränsningsarea:
- \[ \, A \, = \, 2\,\pi\,r\,h \, + 2\,\pi\,r^2 \, = \, 500 \]
Pga begränsningsareans konstanta värde \( \, 500 \, \) blir cylinderns radie störst när höjden blir \( \, 0 \, \).
Därför får vi radiens störst möjliga värde om vi i formeln ovan väljer \( \, h=0 \):
- \[ \, h = 0 \qquad \Longrightarrow \qquad A \, = \, 2\,\pi \cdot \left(r\right)\,^2 \, = \, 500 \qquad \Longrightarrow \qquad r \, = \, \sqrt{500 \over 2\,\pi} \, = \, 8,92 \]
Grafen till vänster visar bivillkoret \( h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \) och till höger målfunktionen \( V(r) \, = \, 250 \, r \, - \, \pi\,r^3 \), båda med definitionsmängden ovan.
Målfunktionens graf till höger bekräftar det algebraiska resultatet från c), nämligen att volymen blir maximal för \( \, r = 5,15 \).
Bivillkorets graf till vänster bekräftar att för \( \, r = 5,15 \, \) höjden blir \( \, \approx \, 10 \) och dessutom att \( \, r \, \) inte kan bli större än \( \, 8,92 \).
e) Resultaten från c) sätts in i målfunktionen för att få cylinderns största volym:
- \[ V(5,15) \, = \, \pi \, \cdot 5,15^2 \, \cdot 10,30 \, = \, 858,23 \]
Konservburkens maximala volym blir \( \; 858,23 \, {\rm cm}^3 \; \).
f) Följande samband råder mellan cylinderns radie \( \; r = 5,15 \, {\rm cm} \; \) och dess höjd \( \; h = 10,30 \, {\rm cm}\)
när volymen till en cylinder med en begränsningsarea på \( \, 500 \, {\rm cm}^2 \, \), maximeras:
- \( 2 \; r \; = \; h \)
Återstår frågan som är föremål för undersökning i övning 9, om samma samband även råder generellt mellan radien \( \; r \; \) och höjden \( \; h \; \) för alla konservburkar med vilken begränsningsarea som helst och maximal volym, nämligen:
- Diametern \( \; = \; \) Höjden
En annan intressant frågeställning är:
Råder även sambandet ovan om man utgår från en konservburk med fast given volym vars materialåtgång ska minimeras?
En närmare undersökning liknande lösningen till Exempel 3 kommer att visa att detta är fallet.
Dvs sambandet ovan är alltid optimalt ur ekonomisk synpunkt.
Ett ekonomiskt exempel
Se övning 7.
Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.