Skillnad mellan versioner av "3.4 Lösning 8c"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (En mellanliggande version av samma användare visas inte) | |||
| Rad 2: | Rad 2: | ||
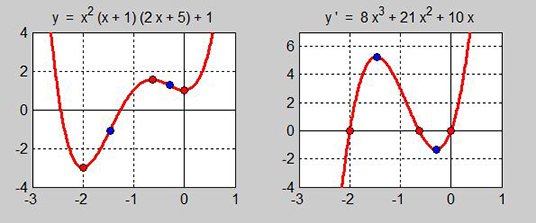
| − | Derivatan har sina extrema i funktionens inflexionspunkter (blåmarkerade) därför att inflexionspunkter förekommer där funktionens andraderivata är <math> \, 0 \, </math> | + | Derivatan har sina extrema i funktionens inflexionspunkter (blåmarkerade) därför att inflexionspunkter förekommer där funktionens andraderivata är <math> \, 0 \, </math>. |
| − | Andraderivatan är | + | Andraderivatan är derivatans derivata. Därför antar derivatan sina extrema i andraderivatans nollställen som i sin tur är funktionens inflexionspunkter, enligt [[3.3_Terasspunkter#Inflexionspunkter|<strong><span style="color:blue">regeln om inflexionspunkter</span></strong>]]. |
Nuvarande version från 21 januari 2017 kl. 20.44
Derivatan har sina extrema i funktionens inflexionspunkter (blåmarkerade) därför att inflexionspunkter förekommer där funktionens andraderivata är \( \, 0 \, \).
Andraderivatan är derivatans derivata. Därför antar derivatan sina extrema i andraderivatans nollställen som i sin tur är funktionens inflexionspunkter, enligt regeln om inflexionspunkter.