Skillnad mellan versioner av "3.2 Lösning 5c"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (5 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
| − | [[Image: Ovn | + | [[Image: Ovn 5c_90.jpg]] |
| + | |||
| + | Följande samband finns mellan funktionens extrempunkter och derivatans nollställen: | ||
Funktionens tre extrempunkter <math> \, x_1 = -2 \, </math>, <math> \, x_2 = 0 \, </math> och <math> \, x_3 = 2 \, </math> är derivatans tre nollställen. | Funktionens tre extrempunkter <math> \, x_1 = -2 \, </math>, <math> \, x_2 = 0 \, </math> och <math> \, x_3 = 2 \, </math> är derivatans tre nollställen. | ||
| − | + | Kring minimipunkten <math> x_1 = -2 \, </math> avtar funktionen till vänster om den och växer till höger, samtidigt som derivatan byter tecken (korsar <math> x</math>-axeln) från <math> \, - \, </math> till <math> \, + \, </math>. Därför är <math> x_1 = -2 \, </math> en minimipunkt. | |
| − | + | Kring maximipunkten <math> x_2 = 0 \, </math> växer funktionen till vänster om den och avtar till höger, samtidigt som derivatan byter tecken (korsar <math> x</math>-axeln) från <math> \, + \, </math> till <math> \, - \, </math>. Därför är <math> x_2 = 0 \, </math> en maximipunkt. | |
| − | + | Kring minimipunkten <math> x_3 = 2 \, </math> avtar funktionen till vänster om den och växer till höger, samtidigt som derivatan byter tecken (korsar <math> x</math>-axeln) från <math> \, - \, </math> till <math> \, + \, </math>. Därför är <math> x_3 = 2 \, </math> en minimipunkt. | |
Nuvarande version från 15 december 2014 kl. 08.18
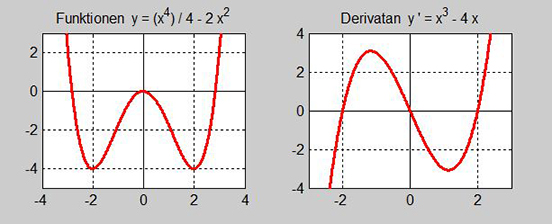
Följande samband finns mellan funktionens extrempunkter och derivatans nollställen:
Funktionens tre extrempunkter \( \, x_1 = -2 \, \), \( \, x_2 = 0 \, \) och \( \, x_3 = 2 \, \) är derivatans tre nollställen.
Kring minimipunkten \( x_1 = -2 \, \) avtar funktionen till vänster om den och växer till höger, samtidigt som derivatan byter tecken (korsar \( x\)-axeln) från \( \, - \, \) till \( \, + \, \). Därför är \( x_1 = -2 \, \) en minimipunkt.
Kring maximipunkten \( x_2 = 0 \, \) växer funktionen till vänster om den och avtar till höger, samtidigt som derivatan byter tecken (korsar \( x\)-axeln) från \( \, + \, \) till \( \, - \, \). Därför är \( x_2 = 0 \, \) en maximipunkt.
Kring minimipunkten \( x_3 = 2 \, \) avtar funktionen till vänster om den och växer till höger, samtidigt som derivatan byter tecken (korsar \( x\)-axeln) från \( \, - \, \) till \( \, + \, \). Därför är \( x_3 = 2 \, \) en minimipunkt.