Skillnad mellan versioner av "3.1 Lösning 9e"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (En mellanliggande version av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
[[Image: Ovn 9e.jpg]] | [[Image: Ovn 9e.jpg]] | ||
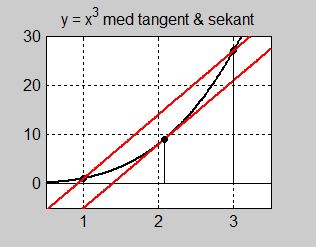
| − | Tangentens lutning i <math> \, x = 2,08 | + | Tangentens lutning i <math> \, x = 2,08 \, </math> är lika stor som sekantens lutning över <math> \, 1 \leq x \leq 3 \, </math>, vilket är ett exempel på medelvärdessatsens utsaga: |
| − | Derivatans medelvärde över intervallet <math> \, 1 \leq x \leq 3 \, </math> (sekantens lutning) är lika stor som derivatan i punkten <math> \, x = 2,08 \, </math> (tangentens lutning) inuti intervallet. | + | Derivatans medelvärde över hela intervallet <math> \, 1 \leq x \leq 3 \, </math> (sekantens lutning) är lika stor som derivatan i punkten <math> \, x = 2,08 \, </math> (tangentens lutning) inuti intervallet. |
Nuvarande version från 5 december 2014 kl. 15.49
Tangentens lutning i \( \, x = 2,08 \, \) är lika stor som sekantens lutning över \( \, 1 \leq x \leq 3 \, \), vilket är ett exempel på medelvärdessatsens utsaga:
Derivatans medelvärde över hela intervallet \( \, 1 \leq x \leq 3 \, \) (sekantens lutning) är lika stor som derivatan i punkten \( \, x = 2,08 \, \) (tangentens lutning) inuti intervallet.