Skillnad mellan versioner av "1.6a Svar 9a"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (2 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
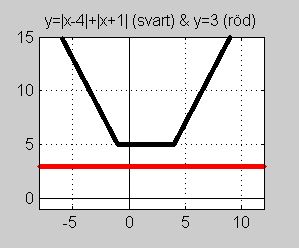
Följande två funktioner ritas i samma koordinatsystem: | Följande två funktioner ritas i samma koordinatsystem: | ||
| − | + | ::<math>\begin{align} y_1 & = | \, x - 4 \, | + | \, x + 1 \, | \qquad {\rm i\;svart} \\ | |
| − | y_2 & = 3 \qquad\qquad\qquad\qquad {\rm i\;rött} | + | y_2 & = 3 \qquad\qquad\qquad\qquad\quad {\rm i\;rött} |
\end{align}</math> | \end{align}</math> | ||
[[Image: Ovn 9.jpg]] | [[Image: Ovn 9.jpg]] | ||
| − | |||
| − | |||
Nuvarande version från 3 september 2014 kl. 11.58
Följande två funktioner ritas i samma koordinatsystem:
- \[\begin{align} y_1 & = | \, x - 4 \, | + | \, x + 1 \, | \qquad {\rm i\;svart} \\ y_2 & = 3 \qquad\qquad\qquad\qquad\quad {\rm i\;rött} \end{align}\]