Skillnad mellan versioner av "1.5a Svar 9a"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (En mellanliggande version av samma användare visas inte) | |||
| Rad 3: | Rad 3: | ||
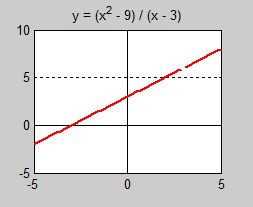
Av grafen kan man inte dra slutsatsen att <math> f(x)\, </math> är kontinuerlig för alla <math> x\, </math>. | Av grafen kan man inte dra slutsatsen att <math> f(x)\, </math> är kontinuerlig för alla <math> x\, </math>. | ||
| − | Funftionsuttrycket <math> {x^2 - 9 \over x-3} \, {\color{White} x} </math> visar att den är diskontinuerlig för <math> x = 3\, </math>. | + | Funftionsuttrycket <big><big><math> {\color{White} x} {x^2 - 9 \over x-3} \, {\color{White} x} </math></big></big> visar att den är diskontinuerlig för <math> x = 3\, </math>. |
<math> f(x)\, </math> är inte definierad för <math> x = 3\, </math>. Därför visar grafen ett "hål" i punkten <math> x = 3\, </math>. | <math> f(x)\, </math> är inte definierad för <math> x = 3\, </math>. Därför visar grafen ett "hål" i punkten <math> x = 3\, </math>. | ||
Nuvarande version från 16 augusti 2014 kl. 19.51
Av grafen kan man inte dra slutsatsen att \( f(x)\, \) är kontinuerlig för alla \( x\, \).
Funftionsuttrycket \( {\color{White} x} {x^2 - 9 \over x-3} \, {\color{White} x} \) visar att den är diskontinuerlig för \( x = 3\, \).
\( f(x)\, \) är inte definierad för \( x = 3\, \). Därför visar grafen ett "hål" i punkten \( x = 3\, \).