Skillnad mellan versioner av "1.5 Övningar till Kontinuerliga och diskreta funktioner"
Taifun (Diskussion | bidrag) m (→Övning 3) |
Taifun (Diskussion | bidrag) m (→Övning 3) |
||
| Rad 50: | Rad 50: | ||
b) Är funktionen <math> f(x)\, </math> definierad för alla <math> x\, </math> i det ritade intervallet? | b) Är funktionen <math> f(x)\, </math> definierad för alla <math> x\, </math> i det ritade intervallet? | ||
| − | c) | + | c) Är funktionen <math> f(x)\, </math> kontinuerlig för alla <math> x\, </math> i det ritade intervallet? |
| − | </div>{{#NAVCONTENT:Svar 3a|1.5a Svar 3a|Svar 3b|1.5a Svar 3b|Svar 3c|1.5a Svar 3c}} | + | d) För vilka <math> x\, </math> är funktionen <math> f(x)\, </math> kontinuerlig och för vilka är den diskontinuerlig?. |
| + | |||
| + | </div>{{#NAVCONTENT:Svar 3a|1.5a Svar 3a|Svar 3b|1.5a Svar 3b|Svar 3c|1.5a Svar 3c|Svar 3d|1.5a Svar 3d}} | ||
Versionen från 10 juli 2014 kl. 18.08
| <-- Förra avsnitt | Teori | Övningar | Fördjupning | Nästa avsnitt --> |
E-övningar: 1-4
Övning 1
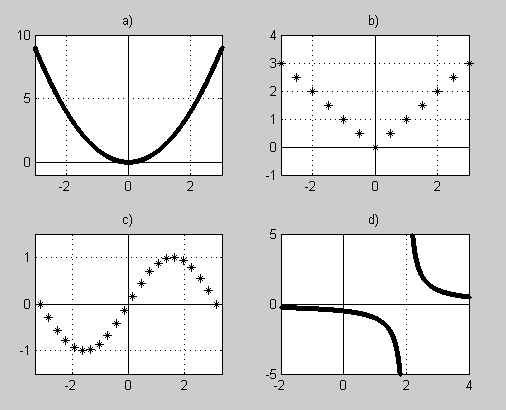
Bestäm för varje graf om den visar en diskret eller en kontinuerlig funktion.
Ange även om och i så fall för vilka \( x \, \) funktionerna har diskontinuiteter.
Motivera dina svar.
Övning 2
Anta att varje ruta i grafen nedan har längdenheten \( 1\, \).
a) Vilket värde kan du läsa av för funktionen \( f(x)\, \) för \( x = a\, \)?
b) Är funktionen \( f(x)\, \) kontinuerlig för alla \( x\, \) i det ritade intervallet?
c) Ange eventuella diskontinuiteter.
Övning 3
Anta att varje ruta i grafen nedan har längdenheten \( 1\, \).
a) Vilket värde kan du läsa av för funktionen \( f(x)\, \) för \( x = a\, \)?
b) Är funktionen \( f(x)\, \) definierad för alla \( x\, \) i det ritade intervallet?
c) Är funktionen \( f(x)\, \) kontinuerlig för alla \( x\, \) i det ritade intervallet?
d) För vilka \( x\, \) är funktionen \( f(x)\, \) kontinuerlig och för vilka är den diskontinuerlig?.
 Hämtar...
Hämtar...