Skillnad mellan versioner av "Fibonaccis talföljd"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (82 mellanliggande versioner av samma användare visas inte) | |||
| Rad 2: | Rad 2: | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{Not selected tab|[ | + | {{Not selected tab|[https://matte5.mathonline.se/index.php/1.7_Geometrisk_summa#Anv.C3.A4ndning_av_geometrisk_summa << Förra avsnitt]}} |
{{Selected tab|[[Fibonaccis talföljd|Genomgång]]}} | {{Selected tab|[[Fibonaccis talföljd|Genomgång]]}} | ||
{{Not selected tab|[[Övningar till Fibonaccis talföljd|Övningar]]}} | {{Not selected tab|[[Övningar till Fibonaccis talföljd|Övningar]]}} | ||
| − | {{Not selected tab|[ | + | {{Not selected tab|[[Grupparbete Ma5|Grupparbete]]}} |
| + | {{Not selected tab|[https://matte1b.mathonline.se/index.php/1.8_Talsystem_med_olika_baser Nästa avsnitt >> ]}} | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| Rad 16: | Rad 17: | ||
<big><big> | <big><big> | ||
| − | Formuleringen | + | Formuleringen ''Samma gäller för de nya paren'' ger upphov till ett '''mönster''' som |
'''upprepas'''. Man återvänder till något som redan gjorts: ett känt förlopp upprepas. | '''upprepas'''. Man återvänder till något som redan gjorts: ett känt förlopp upprepas. | ||
| − | Man kallar det för ett "rekursivt" problem. | + | Man kallar det för ett "rekursivt" problem. Rekursionen används vid problemets lösning. |
| − | Ordet rekursion kommer från det latinska recurrere och betyder att köra igen. | + | Ordet rekursion kommer från det latinska ''recurrere'' och betyder att köra igen. |
| − | + | ||
| − | + | ||
</big></big> | </big></big> | ||
</div> | </div> | ||
| Rad 31: | Rad 30: | ||
= <b><span style="color:#931136">Fibonaccis talföljd</span></b> = | = <b><span style="color:#931136">Fibonaccis talföljd</span></b> = | ||
<div class="ovnC"> | <div class="ovnC"> | ||
| − | [[Image: | + | [[Image: Fib_Talfoljdena.jpg]] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td><big><big><b><span style="color:red"> | + | <td><big><big><b><span style="color:red">Fibonaccis talföljd är varken [https://demo.mathonline.se/index.php?title=1.5_Talf%C3%B6ljder_och_summor#Aritmetiska_talf.C3.B6ljder <span style="color:blue">aritmetisk</span>] eller [https://demo.mathonline.se/index.php?title=1.5_Talf%C3%B6ljder_och_summor#Geometriska_talf.C3.B6ljder <span style="color:blue">geometrisk</span>].</span></b> <br><br> '''Mönstet''' för bildningen av talföljden är snarare:</big></big> <br><br> <div class="border-divblue"> |
<big><b>Summan av två på varandra följande <br> fibonaccital ger nästa fibonaccital.</b></big> | <big><b>Summan av två på varandra följande <br> fibonaccital ger nästa fibonaccital.</b></big> | ||
</div> | </div> | ||
</td> | </td> | ||
| − | <td><math> | + | <td><math> \qquad </math></td> |
<td>[https://sv.wikipedia.org/wiki/Leonardo_Fibonacci [[Image: FibonacciBildb.jpg]]]</td> </tr> | <td>[https://sv.wikipedia.org/wiki/Leonardo_Fibonacci [[Image: FibonacciBildb.jpg]]]</td> </tr> | ||
</table> | </table> | ||
| Rad 50: | Rad 45: | ||
= <b><span style="color:#931136">Fibonaccis rekursionsformel</span></b> = | = <b><span style="color:#931136">Fibonaccis rekursionsformel</span></b> = | ||
| − | <div class=" | + | <div class="ovnA"> |
<div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: FibonacciRekFormel.jpg]]</div> | <div style="border:1px solid black;display:inline-table;margin-left: 0px;"> [[Image: FibonacciRekFormel.jpg]]</div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</div> | </div> | ||
| − | + | <big><big> | |
| − | + | Vi kan använda detta mönster för att bygga en ''algoritm'' för beräkning av fibonaccitalen. | |
| − | + | ||
| − | + | Ännu smartare är det att anlita digitala verktyg för att låta datorn göra jobbet. | |
| − | + | T.ex. lämpar sig kalkylprogrammet Excel utmärkt för en sådan beräkning. | |
| − | + | </big></big> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
= <b><span style="color:#931136">Algoritm för fibonaccitalen i Excel</span></b> = | = <b><span style="color:#931136">Algoritm för fibonaccitalen i Excel</span></b> = | ||
| − | <div class=" | + | <div class="ovnE"> |
| + | <big> | ||
Följande algoritm beskriver hur man kan använda Excel för att låta datorn beräkna fibonaccitalen: | Följande algoritm beskriver hur man kan använda Excel för att låta datorn beräkna fibonaccitalen: | ||
| − | <div class="ovnC" | + | </big> |
| + | <div class="ovnC"> | ||
{{#NAVCONTENT:Klicka här för att följa algoritmen.|Algoritm i Excel}} | {{#NAVCONTENT:Klicka här för att följa algoritmen.|Algoritm i Excel}} | ||
| − | </div> < | + | </div> |
| − | + | <big> | |
I [[1.5_Övningar_till_Kontinuerliga_och_diskreta_funktioner#.C3.96vning_6|<b><span style="color:blue">övning 6</span></b>]] kommer du att behöva använda denna algoritm för att låta datorn beräkna de första <math> \, 24 \, </math> fibonaccitalen. | I [[1.5_Övningar_till_Kontinuerliga_och_diskreta_funktioner#.C3.96vning_6|<b><span style="color:blue">övning 6</span></b>]] kommer du att behöva använda denna algoritm för att låta datorn beräkna de första <math> \, 24 \, </math> fibonaccitalen. | ||
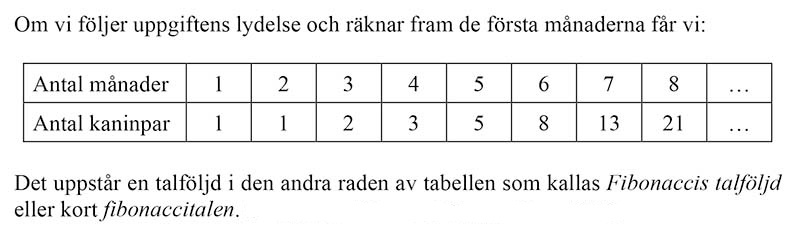
Här är de <math> \, 12 \, </math> första fibonaccitalen beräknade: | Här är de <math> \, 12 \, </math> första fibonaccitalen beräknade: | ||
| − | + | </big> | |
<table> | <table> | ||
<tr> | <tr> | ||
<td> | <td> | ||
| − | + | {| class="wikitable" | |
|- | |- | ||
! Antal månader || Antal kaninpar | ! Antal månader || Antal kaninpar | ||
| Rad 147: | Rad 104: | ||
|} | |} | ||
</td> | </td> | ||
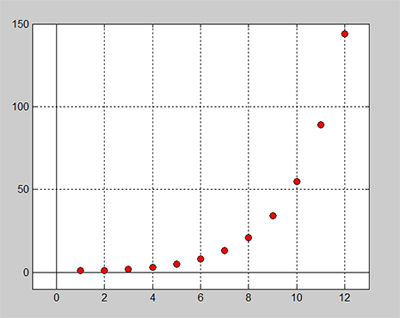
| − | <td> | + | <td> Med denna värdetabell kan vi rita grafen |
| − | | + | till höger som illustrerar fibonaccitalens |
| − | | + | snabba tillväxt. Den horisontella axeln |
| − | | + | visar antal månader och den vertikala |
| − | | + | antal kaninpar. |
| − | | + | |
| − | | + | |
| − | | + | |
| − | | + | Fibonaccitalen bildar en <b><span style="color:red">diskret funktion</span></b> |
| − | | + | därför att dess definitionsmängd är <b><span style="color:red">heltal</span></b>, |
| − | | + | en diskret mängd: månaderna <math> \, {\color{Red} 1}</math><b><span style="color:red">-</span></b><math>{\color{Red} {12}}</math>. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</td> | </td> | ||
| − | <td> | + | <td> [[Image: Fibonacci 400.jpg]]</td> |
</tr> | </tr> | ||
</table> | </table> | ||
| + | <big> | ||
| + | Även grafen består av diskreta dvs åtskilda punkter, inte av en kontinuerlig kurva. | ||
| − | Som man ser ökar kaninpopulationen ganska fort, så att vi nu | + | Som man ser ökar kaninpopulationen ganska fort, så att vi nu kan besvara den inledande frågan: |
| − | Det kommer att finnas <math> | + | Det kommer att finnas <math> 144 </math> kaninpar om ett år. |
| − | </ | + | </big> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</div> | </div> | ||
| − | + | = <b><span style="color:#931136">Fibonaccitalens explicita formel</span></b> = | |
| + | <div class="ovnC"> | ||
| + | Fibonaccis funktion är <b><span style="color:red">rekursiv</span></b>, därför att den anropar sig själv, när den definieras<span>:</span> <math> \qquad\quad F(n) \; = \; F(n-1) \; + \; F(n-2) </math> | ||
| − | + | I en vanlig funktion står <math> F(n) \, </math> till vänster om likhetstecknet och den oberoende variabeln <math> n \, </math> till höger. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Men här står <math> \, F(n) \, </math> på '''båda''' sidor likhetstecknet, även om för olika månader (= argument). | |
| − | + | ||
| + | För att beräkna ett fibonaccital måste man känna till de två föregående. Därav namnet <b><span style="color:red">rekursionsformel</span></b>. | ||
| − | + | Men eftersom vi har de två första <b><span style="color:red">startvärdena</span></b> <math> F(1) = 1 \, </math> och <math> F(2) = 1 \, </math>, kan vi beräkna alla andra rekursivt utgående från dessa. | |
| − | + | Fibonaccis rekursionsformel definierar en funktion som har många intressanta kopplingar till andra delar inom matematiken. | |
| − | + | ||
| − | En | + | En av dem är sambandet mellan fibonaccitalen och det s.k. [http://sv.wikipedia.org/wiki/Gyllene_snittet <b><span style="color:blue">gyllene snittet</span></b>] se [[1.5_Övningar_till_Kontinuerliga_och_diskreta_funktioner#.C3.96vning_6|<b><span style="color:blue">övning 6</span></b>]]. |
| − | + | En annan är följande <b><span style="color:red">explicit formel</span></b> som upptäcktes först 1718, dvs <b><span style="color:red">mer än 500 år senare än själva fibonaccitalen:</span></b> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| Rad 239: | Rad 166: | ||
| − | + | Den explicita formeln ger oss möjligheten att direkt beräkna vilket fibonaccital som helst utan att känna till något föregående fibonaccital. | |
| − | </div | + | |
| + | Den är i själva verket ''lösningen'' till rekursionsformeln, när denna tolkas som en s.k. [http://sv.wikipedia.org/wiki/Differensekvation <b><span style="color:blue">differensekvation</span></b>]. | ||
| + | |||
| + | Differensekvationer är den '''diskreta''' motsvarigheten till differentialekvationer inom '''kontinuerlig''' matematisk analys, som tas upp i kap 3. | ||
| + | |||
| + | I [[1.5_Övningar_till_Kontinuerliga_och_diskreta_funktioner#.C3.96vning_11|<b><span style="color:blue">övning 11</span></b>]] får du till uppgift att bevisa den, vilket kan göras genom att visa att den uppfyller rekursionsformeln (differensekvationen). | ||
| + | </div> | ||
Nuvarande version från 2 november 2024 kl. 09.41
| << Förra avsnitt | Genomgång | Övningar | Grupparbete | Nästa avsnitt >> |
Problemet
Formuleringen Samma gäller för de nya paren ger upphov till ett mönster som
upprepas. Man återvänder till något som redan gjorts: ett känt förlopp upprepas.
Man kallar det för ett "rekursivt" problem. Rekursionen används vid problemets lösning.
Ordet rekursion kommer från det latinska recurrere och betyder att köra igen.
Fibonaccis talföljd
| Fibonaccis talföljd är varken aritmetisk eller geometrisk. Mönstet för bildningen av talföljden är snarare: Summan av två på varandra följande |
\( \qquad \) |  |
Fibonaccis rekursionsformel
Vi kan använda detta mönster för att bygga en algoritm för beräkning av fibonaccitalen.
Ännu smartare är det att anlita digitala verktyg för att låta datorn göra jobbet.
T.ex. lämpar sig kalkylprogrammet Excel utmärkt för en sådan beräkning.
Algoritm för fibonaccitalen i Excel
Följande algoritm beskriver hur man kan använda Excel för att låta datorn beräkna fibonaccitalen:
I övning 6 kommer du att behöva använda denna algoritm för att låta datorn beräkna de första \( \, 24 \, \) fibonaccitalen.
Här är de \( \, 12 \, \) första fibonaccitalen beräknade:
Även grafen består av diskreta dvs åtskilda punkter, inte av en kontinuerlig kurva.
Som man ser ökar kaninpopulationen ganska fort, så att vi nu kan besvara den inledande frågan:
Det kommer att finnas \( 144 \) kaninpar om ett år.
Fibonaccitalens explicita formel
Fibonaccis funktion är rekursiv, därför att den anropar sig själv, när den definieras: \( \qquad\quad F(n) \; = \; F(n-1) \; + \; F(n-2) \)
I en vanlig funktion står \( F(n) \, \) till vänster om likhetstecknet och den oberoende variabeln \( n \, \) till höger.
Men här står \( \, F(n) \, \) på båda sidor likhetstecknet, även om för olika månader (= argument).
För att beräkna ett fibonaccital måste man känna till de två föregående. Därav namnet rekursionsformel.
Men eftersom vi har de två första startvärdena \( F(1) = 1 \, \) och \( F(2) = 1 \, \), kan vi beräkna alla andra rekursivt utgående från dessa.
Fibonaccis rekursionsformel definierar en funktion som har många intressanta kopplingar till andra delar inom matematiken.
En av dem är sambandet mellan fibonaccitalen och det s.k. gyllene snittet se övning 6.
En annan är följande explicit formel som upptäcktes först 1718, dvs mer än 500 år senare än själva fibonaccitalen:
Explicit formel för fibonaccitalen
\( \displaystyle F(n) \; = \; {1\over\sqrt{5}}\,\left({1+\sqrt{5}\over 2}\right)^n\,-\;{1\over\sqrt{5}}\,\left({1-\sqrt{5}\over 2}\right)^n\; , \qquad n \;\mbox{heltal } \geq 1 \)
Den explicita formeln ger oss möjligheten att direkt beräkna vilket fibonaccital som helst utan att känna till något föregående fibonaccital.
Den är i själva verket lösningen till rekursionsformeln, när denna tolkas som en s.k. differensekvation.
Differensekvationer är den diskreta motsvarigheten till differentialekvationer inom kontinuerlig matematisk analys, som tas upp i kap 3.
I övning 11 får du till uppgift att bevisa den, vilket kan göras genom att visa att den uppfyller rekursionsformeln (differensekvationen).
Copyright © 2024 Lieta AB. All Rights Reserved.


 Hämtar...
Hämtar...