Skillnad mellan versioner av "1.5 Kontinuerliga och diskreta funktioner"

Från Mathonline
Hoppa till: navigering, sök
m
m
 
(181 mellanliggande versioner av samma användare visas inte)
Rad 1: Rad 1:
 +
__NOTOC__
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 
| style="border-bottom:1px solid #797979" width="5px" |  
 
| style="border-bottom:1px solid #797979" width="5px" |  
−
{{Not selected tab|[[1.1 Polynom|<-- Förra demoavsnitt]]}}
+
{{Not selected tab|[[1.4 Talet e och den naturliga logaritmen| <<&nbsp;&nbsp;Förra demoavsnitt]]}}
 
{{Selected tab|[[1.5 Kontinuerliga och diskreta funktioner|Genomgång]]}}
 
{{Selected tab|[[1.5 Kontinuerliga och diskreta funktioner|Genomgång]]}}
 
{{Not selected tab|[[1.5 Övningar till Kontinuerliga och diskreta funktioner|Övningar]]}}
 
{{Not selected tab|[[1.5 Övningar till Kontinuerliga och diskreta funktioner|Övningar]]}}
 
{{Not selected tab|[[1.5 Fördjupning till Kontinuerliga och diskreta funktioner|Fördjupning]]}}
 
{{Not selected tab|[[1.5 Fördjupning till Kontinuerliga och diskreta funktioner|Fördjupning]]}}
−
{{Not selected tab|[[Diagnosprov 1 i Matte 3 kap 1 Algebra och funktioner|Diagnosprov kap 1 -->]]}}
+
{{Not selected tab|[[1.6 Absolutbelopp|Nästa demoavsnitt&nbsp;&nbsp;>> ]]}}
−
<!-- {{Not selected tab|[[1.6 Absolutbelopp|Nästa avsnitt --> <!-- ]]}} -->
+
<!-- {{Not selected tab|[[2.1 Introduktion till derivata|Nästa demoavsnitt <math> \pmb{\to} </math>]]}} -->
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
| style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 
|}
 
|}
  
 +
 +
<big>
 +
I matematiken betyder <b><span style="color:red">diskret</span></b> åtskild, avgränsad eller separerad och är motsatsen till kontinuerlig.
 +
 +
Heltalen bildar en diskret mängd därför att de är avgränsade från sina "grannar" på tallinjen med ett helsteg. Det finns inget heltal mellan <math> \, 2 \, </math> och <math> \, 3 \, </math> och inte heller mellan de andra heltalen.
 +
 +
"Antal" är alltid heltal och därmed diskret. Därför är t.ex. "antal ägg" diskret: Det finns inga halva eller bråkdel ägg.
 +
</big>
  
  
−
[[Media: Lektion 8 Kontin. & diskreta funktioner Rutaa.pdf|<strong><span style="color:blue">Lektion 8 Kontinuerliga & diskreta funktioner</span></strong>]]
 
−
__NOTOC__  <!-- __TOC__ -->
 
−
<div class="exempel">
 
 
== <b><span style="color:#931136">Exempel 1 Diskret funktion</span></b> ==
 
== <b><span style="color:#931136">Exempel 1 Diskret funktion</span></b> ==
 +
<div class="ovnA">
 
<big>
 
<big>
−
En torghandlare säljer ägg för <math> \, 3 </math> kr per styck.
 
−
 
−
Ställ upp och rita grafen till prisfunktionen som beskriver priset <math> y \, </math> i kr som en funktion av antalet <math> n \, </math> sålda ägg.
 
 
<table>
 
<table>
 
<tr>
 
<tr>
−
   <td>
+
   <td>En torghandlare säljer ägg för <math> \, 3 </math> kr per styck.
−
'''Lösning:'''
+
  
 
<math> {\color{Red} 1} \; </math> ägg kostar <math> {\color{Red} 1} \cdot 3 \;{\rm kr,} </math>
 
<math> {\color{Red} 1} \; </math> ägg kostar <math> {\color{Red} 1} \cdot 3 \;{\rm kr,} </math>
Rad 29: Rad 32:
 
<math> {\color{Red} 2} \; </math> ägg kostar <math> {\color{Red} 2} \cdot 3 \;{\rm kr,} </math>
 
<math> {\color{Red} 2} \; </math> ägg kostar <math> {\color{Red} 2} \cdot 3 \;{\rm kr,} </math>
  
−
<math> {\color{Red} 3} \; </math> ägg kostar <math> {\color{Red} 3} \cdot 3 \;{\rm kr,} </math>
+
<math> {\color{Red} 3} \; </math> ägg kostar <math> {\color{Red} 3} \cdot 3 \;{\rm kr,} \qquad \cdots </math>
−
 
+
−
<math> \qquad \cdots </math>
+
  
 
<math> {\color{Red} n} \; </math> ägg kostar <math> {\color{Red} n} \cdot 3 \;{\rm kr} </math> eller <math> 3\;{\color{Red} n} \;{\rm kr.} </math>
 
<math> {\color{Red} n} \; </math> ägg kostar <math> {\color{Red} n} \cdot 3 \;{\rm kr} </math> eller <math> 3\;{\color{Red} n} \;{\rm kr.} </math>
Rad 37: Rad 38:
 
Därför är prisfunktionen:
 
Därför är prisfunktionen:
  
−
<div style="border:1px solid black;
+
<div class="smallBoxVariant"><math> y = 3\;{\color{Red} n} \, , \quad  
−
display:inline-block !important;
+
  {\rm där } \quad {\color{Red} n}\,= {\rm {\color{Red} {heltal}}\,.} </math></div>
−
margin-left: 0px !important;
+
−
padding:10px 20px 10px 20px;
+
−
-webkit-border-radius: 10px;
+
−
-moz-border-radius: 5px;
+
−
border-radius: 5px;"><math> y = 3\;{\color{Red} n} \, , \quad  
+
−
  {\rm där } \quad {\color{Red} n}\,= {\rm {\color{Red} {heltal}}\,.} </math>
+
−
</div>
+
 
</td>
 
</td>
−
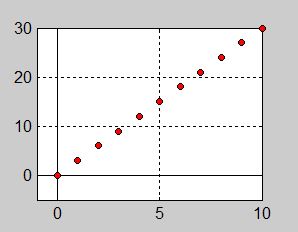
   <td> &nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  &nbsp; [[Image: Diskret prisfunktion agg 50.jpg]]</td>
+
   <td> &nbsp;  &nbsp; &nbsp;  &nbsp; [[Image: Diskret_prisfunktion_agg.jpg]]</td>
−
   <td> &nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  &nbsp; Grafen till prisfunktionen visar priset <math> y \, </math> i kr (vertikal axel)
+
   <td> &nbsp;  &nbsp; &nbsp;  &nbsp; Grafen till prisfunktionen visar priset <math> y \, </math> i kr (vertikal axel)
 +
 
 +
&nbsp;  &nbsp; &nbsp;  &nbsp; som en funktion av <b><span style="color:red">antalet</span></b> <math> {\color{Red} n} \, </math> (horisontell axel).
  
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  &nbsp; som en funktion av <strong><span style="color:red">antalet</span></strong> <math> {\color{Red} n} \, </math> (horisontell axel).
 
  
 +
&nbsp;  &nbsp; &nbsp;  &nbsp; Grafen till en diskret funktion ritas med <b><span style="color:red">separerade</span></b>
  
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  &nbsp; En diskret funktions graf ritas med separerade
+
&nbsp;  &nbsp; &nbsp;  &nbsp; <b><span style="color:red">punkter</span></b> och inte med en genomdragen linje.
  
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  &nbsp; prickar och inte med en genomdragen linje.
 
  
 +
&nbsp;  &nbsp; &nbsp;  &nbsp; För att rita en diskret funktions graf måste man
  
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  &nbsp; För att rita en diskret funktions graf måste man lyfta pennan.
+
&nbsp;  &nbsp; &nbsp;  &nbsp; lyfta pennan.
 
   </td>
 
   </td>
 
</tr>
 
</tr>
 
</table>
 
</table>
 +
<math> \quad\; y \, </math> är priset i kr. <math> \quad\; \color{Red} n \, </math> är antalet ägg.
  
−
 
+
<math> y = 3\;{\color{Red} n} </math> är en <div class="smallBox"><b><span style="color:red">diskret funktion</span></b></div> &nbsp;&nbsp; därför att dess <b><span style="color:red">definitionsmängd</span></b> är en <div class="smallBox"><b><span style="color:red">diskret mängd</span></b></div> &nbsp;&nbsp; nämligen alla <b><span style="color:red"> heltal </span></b> <math> {\color{Red} n} \geq 0\, </math>.  
−
<math> y = 3\;{\color{Red} n} </math> är en <div style="border:1px solid black;
+
−
display:inline-block !important;
+
−
margin-left: 10px !important;
+
−
padding:10px 10px 10px 10px;
+
−
-webkit-border-radius: 10px;
+
−
-moz-border-radius: 5px;
+
−
border-radius: 5px;"><strong>diskret funktion</strong></div> &nbsp;&nbsp; därför att dess definitionsmängd: alla <math> {\color{Red} n} \geq 0\, </math> med <math> {\color{Red} n} \, </math> <strong><span style="color:red"> = heltal </span></strong> är en diskret mängd.  
+
 
</big>
 
</big>
−
</div> <!-- exempel -->
+
</div>
  
  
−
<div class="tolv"> <!-- tolv1 -->
+
<big>
−
I matematiken betyder <strong><span style="color:red">diskret</span></strong> åtskild, avgränsad eller separerad och är motsatsen till kontinuerlig. Heltalen bildar en diskret mängd därför att de är avgränsade från sina "grannar" på tallinjen med ett helsteg. Det finns inget heltal mellan <math> \, 2 \, </math> och <math> \, 3 \, </math> och inte heller mellan de andra heltalen. "Antal" är alltid heltal och därmed diskret. Därför är även "antal ägg" diskret: Det finns inga halva eller bråkdel ägg.
+
I matematiken betyder <b><span style="color:red">kontinuerlig</span></b> sammanhängande och är motsatsen till diskret.
−
</div> <!-- tolv1 -->
+
 
 +
De rationella och reella talen är kontinuerliga mängder därför att mellan två sådana tal - hur nära varandra de än mår vara - finns alltid oändligt många andra tal.  
 +
 
 +
En mängd vätska t.ex. är kontinuerlig: Det finns halva eller alla möjliga bråkdelar av mängden.
 +
</big>
  
  
−
<div class="exempel">
 
 
== <b><span style="color:#931136">Exempel 2 Kontinuerlig funktion</span></b> ==
 
== <b><span style="color:#931136">Exempel 2 Kontinuerlig funktion</span></b> ==
 +
<div class="ovnC">
 
<big>
 
<big>
 
<table>
 
<table>
Rad 89: Rad 83:
  
 
granatäppeljuice för <math> \, 30 </math> kr per liter.  
 
granatäppeljuice för <math> \, 30 </math> kr per liter.  
−
 
−
Ställ upp och rita grafen till prisfunktionen
 
−
 
−
som beskriver priset <math> y \, </math> kr för <math> x \, </math> liter.
 
−
 
−
'''Lösning:'''
 
  
 
Av samma anledning som i <b><span style="color:#931136">Exempel 1</span></b> är
 
Av samma anledning som i <b><span style="color:#931136">Exempel 1</span></b> är
Rad 100: Rad 88:
 
prisfunktionen här:
 
prisfunktionen här:
  
−
<div style="border:1px solid black;
+
<div class="smallBoxVariant"><math> y = 30\;{\color{Red} x} \, , \quad  
−
display:inline-block !important;
+
−
margin-left: 0px !important;
+
−
padding:10px 20px 10px 20px;
+
−
-webkit-border-radius: 10px;
+
−
-moz-border-radius: 5px;
+
−
border-radius: 5px;"><math> y = 30\;{\color{Red} x} \, , \quad  
+
 
  {\rm där } \quad {\color{Red} x}\,= {\rm {\color{Red} {reellt\;tal}}\,.} </math>
 
  {\rm där } \quad {\color{Red} x}\,= {\rm {\color{Red} {reellt\;tal}}\,.} </math>
 
</div>
 
</div>
 +
<math> \quad\; y \, </math> är priset i kr. <math> \quad\;\;\; \color{Red} x \, </math> är mängden i liter.
 +
 +
<math> y = 30\;{\color{Red} x} </math> är en <div class="smallBox"><b><span style="color:red">kontinuerlig funktion</span></b></div>
 
</td>
 
</td>
−
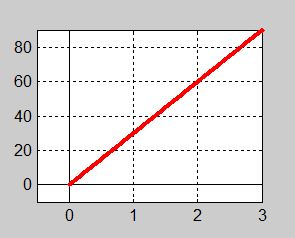
   <td> &nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  [[Image: Kontinuerlig prisfunktion ris 50.jpg]]</td>
+
   <td> &nbsp;  &nbsp; &nbsp;  &nbsp; [[Image: Kontinuerlig_prisfunktion_ris.jpg]]</td>
−
   <td> &nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  Grafen till Funktionen <math> y = 30\;{\color{Red} x} </math> visar priset <math> y \, </math>  
+
   <td> &nbsp;  &nbsp; &nbsp;  &nbsp; Grafen till Funktionen <math> y = 30\;{\color{Red} x} </math> visar priset <math> y \, </math>  
  
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  som en funktion av <strong><span style="color:red">volymen</span></strong> <math> {\color{Red} x} </math> (i liter).
+
&nbsp;  &nbsp; &nbsp;  &nbsp; som en funktion av <b><span style="color:red">mängden</span></b> <math> {\color{Red} x} </math> (i liter).
  
  
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  En kontinuerlig funktions graf ritas med en  
+
&nbsp;  &nbsp; &nbsp;  &nbsp; Grafen till en kontinuerlig funktion ritas med en  
  
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  genomdragen linje och inte med prickar.
+
&nbsp;  &nbsp; &nbsp;  &nbsp; <b><span style="color:red">genomdragen linje</span></b> och inte med separerade punkter.
  
  
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  En kontinuerlig funktions graf kan man rita
+
&nbsp;  &nbsp; &nbsp;  &nbsp; En kontinuerlig funktions graf kan man rita
  
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  utan att lyfta pennan.
+
&nbsp;  &nbsp; &nbsp;  &nbsp; utan att lyfta pennan.
 
   </td>
 
   </td>
 
</tr>
 
</tr>
 
</table>
 
</table>
−
 
+
därför att dess <b><span style="color:red">definitionsmängd</span></b> är en <div class="smallBox"><b><span style="color:red">kontinuerlig mängd</span></b></div>&nbsp;&nbsp;&nbsp;&nbsp;nämligen alla <b><span style="color:red"> reella tal</span></b> <math> {\color{Red} x} \geq 0\, </math>.
−
 
+
−
<math> y = 30\;{\color{Red} x} </math> med <math> {\color{Red} x} \, </math> <strong><span style="color:red"> = reellt tal </span></strong> är en <div style="border:1px solid black;
+
−
display:inline-block !important;
+
−
margin-left: 10px !important;
+
−
padding:10px 10px 10px 10px;
+
−
-webkit-border-radius: 10px;
+
−
-moz-border-radius: 5px;
+
−
border-radius: 5px;"><strong>kontinuerlig funktion</strong></div>&nbsp;&nbsp;&nbsp;&nbsp;därför att dess definitionsmängd: alla <math> {\color{Red} x} \geq 0\, </math> med <math> {\color{Red} x} \, </math> <strong><span style="color:red"> = volymen</span></strong> (i liter) är en kontinuerlig mängd.  
+
 
</big>
 
</big>
−
</div> <!-- exempel -->
+
</div>
−
 
+
  
 
<div class="tolv"> <!-- tolv2 -->
 
<div class="tolv"> <!-- tolv2 -->
−
I matematiken betyder <strong><span style="color:red">kontinuerlig</span></strong> sammanhängande och är motsatsen till diskret. De rationella och reella talen är kontinuerliga mängder därför att mellan två sådana tal - hur nära varandra de än mår vara - finns alltid oändligt många andra tal.  
+
Kontinuerliga funktioner används ofta som matematiska modeller för att beskriva verkligheten. Men i vissa fall föredrar man diskreta modeller som studeras i en speciell disciplin
  
−
Kontinuitet är en matematisk abstraktion som endast förekommer i talmängder eller andra matematiska objekt. Kontinuerliga funktioner är matematiska modeller som man i regel använder för att beskriva verkligheten. Men i vissa fall föredrar man diskreta modeller. Sådana modeller studeras i en speciell disciplin av matematiken som heter [http://sv.wikipedia.org/wiki/Diskret_matematik <strong><span style="color:blue">Diskret matematik</span></strong>].
+
som heter [http://sv.wikipedia.org/wiki/Diskret_matematik <b><span style="color:blue">Diskret matematik</span></b>]. Talteori, mängdlära  och kombinatorik är typiska ämnen i Diskret matematik som behandlas i Matte 5.
−
</div> <!-- tolv2 -->
+
−
<!--
+
−
'''Anmärkning 1:''' I exemplet ovan har man försummat att ett riskorn väger ca. 0,02 g. Eftersom man inte kan dela ett riskorn kan man - rent teoretiskt - hävda att funktionen i exemplet också är diskret. Vikten växer nämligen inte kontinuerligt utan med ett diskret steg på 0,02 g. Och därmed växer även priset med ett diskret steg på 0,02 g * 3 ören/g = 0,06 ören. Men i praktiken kan man kanske förlåta denna försummelse. Genom att fundera vidare i dessa banor lämnar man matematiken och kommer in i filosofiska diskussioner. Ett annat intressant problem i detta sammanhang är: Är tiden diskret eller kontinuerlig? Inte sättet att mäta den utan tiden i sig. Vi har som vanligt i filosofin inget svar på denna fråga.
+
−
 
+
−
'''Anmärkning 2:''' I verkligheten finns det - exakt talat - inga kontinuerliga mängder, vilket visar betydelsen av diskreta funktioner.
+
−
-->
+
−
 
+
−
 
+
−
== <b><span style="color:#931136">Digital beräkning av en diskret funktion (Fibonaccis problem)</span></b> ==
+
−
 
+
−
<div class="tolv"> <!-- tolv3 -->
+
−
Ett exempel på problem som med fördel kan modelleras med diskreta funktioner är följande uppgift som den italienske matematikern [http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibBio.html <strong><span style="color:blue">Leonardo Pisano Fibonacci</span></strong>] år 1202 formulerade i sin bok [http://liberabaci.blogspot.se/ <strong><span style="color:blue">Liber abaci</span></strong>] (Boken om räknekonsten).
+
−
 
+
−
[http://www.math.fau.edu/MathCircle_at_FAU/MC130713Problems.pdf <strong><span style="color:blue">Fibonaccis problem</span></strong>] handlar om kaniners fortplantning:
+
−
 
+
−
:::::[[Image: Fibonacci problem 60.jpg]]
+
−
 
+
−
Om vi följer uppgiftens lydelse kan vi räkna fram de första månadernas kaninpopulation:
+
−
 
+
−
De två första månaderna finns det <math> \, {\color{Red} 1} \, </math> kaninpar. De föder sitt första barnpar först efter 2 månader dvs i månad nr 3, varför det finns <math> \, {\color{Red} 2} \, </math> kaninpar i månad 3. I månad 4 föder det första paret sitt andra barnpar, varför det finns <math> \, {\color{Red} 3} \, </math> par i månad 4. I månad 5 föder det första paret sitt tredje barnpar, men även deras första barnpar föder ett nytt par, eftersom det har gått 2 månader sedan deras födelse. Därför finns det <math> \, {\color{Red} 5} \, </math> par i månad 5. Osv. <math> \cdots </math>.
+
−
 
+
−
Talföljden <math> \, {\color{Red} 1}, \, {\color{Red} 1}, \, {\color{Red} 2}, \, {\color{Red} 3}, \, {\color{Red} 5}, \, \ldots \, </math> som representerar antal kaninpar varje månad kallas [http://sv.wikipedia.org/wiki/Fibonaccital <strong><span style="color:blue">fibonaccitalen</span></strong>].
+
−
 
+
−
Undersöker man talföljden noga kan man se följande enkelt mönster:
+
−
 
+
−
<div class="exempel">
+
−
'''Mönster:'''
+
−
::::Summan av två på varandra följande fibonaccital ger nästa fibonaccital.
+
 
</div>
 
</div>
  
−
Praktiskt taget blir det allt svårare att hålla reda på antal kaninpar när antalet månader växer. Vi ska använda digitala verktyg för att låta datorn sköta beräkningsarbetet. Mönstret ovan kan anses som en algoritm, dvs ett tillvägagångssätt, för att programmera datorn. T.ex. lämpar sig kalkylprogrammet Excel bra för en sådan beräkning:
 
−
</div> <!-- tolv3 -->
 
−
 
−
 
−
== <b><span style="color:#931136">Algoritm för fibonaccitalen i Excel</span></b> ==
 
−
<div class="tolv"> <!-- tolv4 -->
 
−
{{#NAVCONTENT:Klicka här för att följa algoritmen.|Algoritm i Excel}}
 
−
 
−
Med algoritmen ovan beräknas de <math> \, 12 \, </math> första fibonaccitalen till:
 
−
 
−
<table>
 
−
<tr>
 
−
  <td>
 
−
:{| class="wikitable"
 
−
|-
 
−
! Antal månader || Antal kaninpar
 
−
|-
 
−
| align=center| <math> {\color{Red} 1}\, </math> ||align=center| <math> 1\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} 2}\, </math> ||align=center| <math> 1\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} 3}\, </math> ||align=center| <math> 2\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} 4}\, </math> ||align=center| <math> 3\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} 5}\, </math> ||align=center| <math> 5\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} 6}\, </math> ||align=center| <math> 8\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} 7}\, </math> ||align=center| <math> 13\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} 8}\, </math> ||align=center| <math> 21\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} 9}\, </math> ||align=center| <math> 34\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} {10}}\, </math> ||align=center| <math> 55\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} {11}}\, </math> ||align=center| <math> 89\, </math>
 
−
|-
 
−
| align=center| <math> {\color{Red} {12}}\, </math> ||align=center| <math> 144\, </math>
 
−
|}
 
−
</td>
 
−
  <td> &nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  Till höger har grafen till de <math> \, 12 \, </math> första
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  fibonaccitalen ritats: Antalet månader
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  på den horisontella och antalet kaninpar
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  på den vertikala axeln.
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp; 
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp; 
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp; 
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp; 
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp; 
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp; 
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  Fibonaccitalen bildar en <strong><span style="color:red">diskret funktion</span></strong>
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  därför att dess definitionsmängd - bestående
 
−
 
−
&nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  av månaderna <math> \, {\color{Red} {1 - 12}} \, </math> - är <strong><span style="color:red">heltal</span></strong>.
 
−
  </td>
 
−
  <td> &nbsp;  &nbsp; &nbsp;  &nbsp; &nbsp;  [[Image: Fibonacci 465p.jpg]]</td>
 
−
</tr>
 
−
</table>
 
−
 
−
Som man ser växer fibonaccitalen, dvs ökar kaninpopulationen, ganska fort, så att vi nu äntligen kan besvara den inledande frågan:
 
−
 
−
 
−
<div class="border-div2">
 
−
<big>Det kommer att finnas <math> 144 \, </math> kaninpar om ett år.</big>
 
−
</div>
 
−
</div> <!-- tolv4 -->
 
−
 
−
 
−
== <b><span style="color:#931136">Fibonaccis funktion</span></b> ==
 
−
 
−
<div class="tolv"> <!-- tolv5 -->
 
−
För att beskriva detta mönster inför vi beteckningarna:
 
−
 
−
::::<math> n \, = \, {\rm Antalet\;månader} </math>
 
−
 
−
::::<math> F(n)\, = \, {\rm Antalet\;kaninpar\;i\;månaden} \, n </math>
 
−
 
−
De första två fibonaccitalen tar vi från tabellen ovan. Det är <math> 1\, </math> och <math> 1\, </math>. Resten - det som följer - är en ren översättning av mönstrets svenska till matematiskt språk som ger oss <strong><span style="color:red">Fibonaccis funktion</span></strong>:
 
−
 
−
 
−
<div class="border-div"><big><math>  F(n) \, = \, \begin{cases} 1                & \mbox{om } n = 1                                    \\
 
−
                                                                1                & \mbox{om } n = 2 \qquad\qquad n \quad\mbox{heltal}  \\
 
−
                                                                F(n-1) + F(n-2)  & \mbox{om } n = 3,\,4,\,5,\,\cdots
 
−
                                                  \end{cases}
 
−
                        </math></big>
 
−
</div>
 
  
 +
== <b><span style="color:#931136">[[Fibonaccis talföljd|<span style="color:blue">Exempel 3 Fibonaccis talföljd</span>]] </span></b> ==
  
−
Så här brukar man skriva för att för en och samma funktion definiera olika funktionsuttryck i olika delar av dess definitionsmängd. Kanske blir det enklare att förstå den om den skrivs på följande förenklat sätt: 
+
<br>
  
−
:::::<math>\begin{array}{rcl}  F(1) & = & 1  \\
 
−
                              F(2) & = & 1  \\
 
−
                              F(n) & = & F(n-1) + F(n-2) \qquad \mbox{om } n = 3,\,4,\,5,\,\cdots
 
−
          \end{array}</math>
 
  
−
Formeln ovan definierar en <strong><span style="color:red">diskret funktion</span></strong> eftersom <math> n\, = \, </math> antalet kaninpar är heltal. Den kallas [http://www.wolframalpha.com/input/?i=fibonacci+function <strong><span style="color:blue">Fibonaccis funktion</span></strong>].
 
  
−
De första raderna i definitionen ovan säger att de första två fibonaccitalen är 1 och 1. Den andra raden säger att det n-te fibonaccitalet är summan av de två föregående, vilket är bara en annan formulering av samma mönster vi upptäckte tidigare.
 
  
−
En intressant egenskap av Fibonaccis funktion är att den är <strong><span style="color:red">rekursiv</span></strong>, vilket betyder att den i sin definition anropar sig själv, fast med olika argument, dvs ett värde beräknas med hjälp av föregående värden. För att se detta titta på [[1.5_Kontinuerliga_och_diskreta_funktioner#Fibonaccis_funktion|<strong><span style="color:blue">Fibonaccis funktion</span></strong>]]: I en vanlig funktion står <math> F(n) \, </math> vänster om likhetstecknet och den oberoende variabeln <math> n \, </math> höger om likhetstecknet. Men här står <math> F(n) \, </math> på båda sidor likhetstecknet, fast för olika månader (= argument). För att beräkna ett fibonaccital måste man känna till de två föregående. Men eftersom vi har de två första <math> F(1) = 1 \, </math> och <math> F(2) = 1 \, </math>, s.k. <strong><span style="color:red">startvärden</span></strong>, kan vi beräkna alla andra successivt dvs rekursivt utgående från dessa startvärden. Att <math> F(n) \, </math> anropas på båda sidor likhetstecknet är just den rekursiva egenskapen. Därför kallas Fibonaccis formel även <strong><span style="color:red">Fibonaccis rekursionsformel</span></strong>.
 
  
−
För ett intressant samband mellan fibonaccitalen och det s.k. [http://sv.wikipedia.org/wiki/Gyllene_snittet <strong><span style="color:blue">gyllene snittet</span></strong>] se [[1.5_Övningar_till_Kontinuerliga_och_diskreta_funktioner#.C3.96vning_6|<strong><span style="color:blue">övning 6</span></strong>]].
 
−
</div> <!-- tolv5 -->
 
  
  
−
== Internetlänkar ==
+
== <b><span style="color:#931136">Internetlänkar</span></b> ==
  
 
http://www.youtube.com/watch?v=SKRjz2aTqCY
 
http://www.youtube.com/watch?v=SKRjz2aTqCY
Rad 313: Rad 154:
  
  
−
[[Matte:Copyrights|Copyright]] © 2011-2015 Math Online Sweden AB. All Rights Reserved.
+
[[Matte:Copyrights|Copyright]] © 2021 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved.

Nuvarande version från 1 juli 2024 kl. 11.25

        <<  Förra demoavsnitt          Genomgång          Övningar          Fördjupning          Nästa demoavsnitt  >>      


I matematiken betyder diskret åtskild, avgränsad eller separerad och är motsatsen till kontinuerlig.

Heltalen bildar en diskret mängd därför att de är avgränsade från sina "grannar" på tallinjen med ett helsteg. Det finns inget heltal mellan \( \, 2 \, \) och \( \, 3 \, \) och inte heller mellan de andra heltalen.

"Antal" är alltid heltal och därmed diskret. Därför är t.ex. "antal ägg" diskret: Det finns inga halva eller bråkdel ägg.


Exempel 1 Diskret funktion

En torghandlare säljer ägg för \( \, 3 \) kr per styck.

\( {\color{Red} 1} \; \) ägg kostar \( {\color{Red} 1} \cdot 3 \;{\rm kr,} \)

\( {\color{Red} 2} \; \) ägg kostar \( {\color{Red} 2} \cdot 3 \;{\rm kr,} \)

\( {\color{Red} 3} \; \) ägg kostar \( {\color{Red} 3} \cdot 3 \;{\rm kr,} \qquad \cdots \)

\( {\color{Red} n} \; \) ägg kostar \( {\color{Red} n} \cdot 3 \;{\rm kr} \) eller \( 3\;{\color{Red} n} \;{\rm kr.} \)

Därför är prisfunktionen:

\( y = 3\;{\color{Red} n} \, , \quad {\rm där } \quad {\color{Red} n}\,= {\rm {\color{Red} {heltal}}\,.} \)
         Diskret prisfunktion agg.jpg         Grafen till prisfunktionen visar priset \( y \, \) i kr (vertikal axel)

        som en funktion av antalet \( {\color{Red} n} \, \) (horisontell axel).


        Grafen till en diskret funktion ritas med separerade

        punkter och inte med en genomdragen linje.


        För att rita en diskret funktions graf måste man

        lyfta pennan.

\( \quad\; y \, \) är priset i kr. \( \quad\; \color{Red} n \, \) är antalet ägg.

\( y = 3\;{\color{Red} n} \) är en
diskret funktion
   därför att dess definitionsmängd är en
diskret mängd
   nämligen alla heltal \( {\color{Red} n} \geq 0\, \).


I matematiken betyder kontinuerlig sammanhängande och är motsatsen till diskret.

De rationella och reella talen är kontinuerliga mängder därför att mellan två sådana tal - hur nära varandra de än mår vara - finns alltid oändligt många andra tal.

En mängd vätska t.ex. är kontinuerlig: Det finns halva eller alla möjliga bråkdelar av mängden.


Exempel 2 Kontinuerlig funktion

En annan torghandlare säljer färskpressad

granatäppeljuice för \( \, 30 \) kr per liter.

Av samma anledning som i Exempel 1 är

prisfunktionen här:

\( y = 30\;{\color{Red} x} \, , \quad {\rm där } \quad {\color{Red} x}\,= {\rm {\color{Red} {reellt\;tal}}\,.} \)

\( \quad\; y \, \) är priset i kr. \( \quad\;\;\; \color{Red} x \, \) är mängden i liter.

\( y = 30\;{\color{Red} x} \) är en
kontinuerlig funktion
         Kontinuerlig prisfunktion ris.jpg         Grafen till Funktionen \( y = 30\;{\color{Red} x} \) visar priset \( y \, \)

        som en funktion av mängden \( {\color{Red} x} \) (i liter).


        Grafen till en kontinuerlig funktion ritas med en

        genomdragen linje och inte med separerade punkter.


        En kontinuerlig funktions graf kan man rita

        utan att lyfta pennan.

därför att dess definitionsmängd är en
kontinuerlig mängd
    nämligen alla reella tal \( {\color{Red} x} \geq 0\, \).

Kontinuerliga funktioner används ofta som matematiska modeller för att beskriva verkligheten. Men i vissa fall föredrar man diskreta modeller som studeras i en speciell disciplin

som heter Diskret matematik. Talteori, mängdlära och kombinatorik är typiska ämnen i Diskret matematik som behandlas i Matte 5.


Exempel 3 Fibonaccis talföljd





Internetlänkar

http://www.youtube.com/watch?v=SKRjz2aTqCY

http://www.youtube.com/watch?v=cvnG0YWPLjQ

http://www.sigma8.se/dokument/TabyFriskola_Amnesrapport_OK_2012.pdf

http://www03.edu.fi/svenska/oppimateriaalit/arkimatematiikkaa/fibona.html

http://paranormal.se/topic/det_gyllene_snittet.html

http://www.math.fau.edu/MathCircle_at_FAU/MC130713Problems.pdf





Copyright © 2021 TechPages AB. All Rights Reserved.

Hämtad från "https://minidemo.mathonline.se/index.php?title=1.5_Kontinuerliga_och_diskreta_funktioner&oldid=29389"