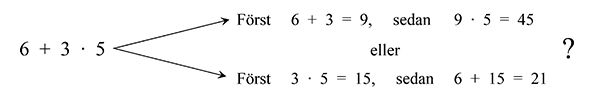Skillnad mellan versioner av "1.2 Räkneordning"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (92 mellanliggande versioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | ||
| style="border-bottom:1px solid #797979" width="5px" | | | style="border-bottom:1px solid #797979" width="5px" | | ||
| − | {{Not selected tab|[[1.1 Om tal|< | + | {{Not selected tab|[[1.1 Om tal| << Förra avsnitt]]}} |
{{Selected tab|[[1.2 Räkneordning|Genomgång]]}} | {{Selected tab|[[1.2 Räkneordning|Genomgång]]}} | ||
| − | {{Not selected tab|[[1.2 Övningar till Räkneordning|Övningar]]}} | + | {{Not selected tab|[[1.2 Övningar till Räkneordning|Övningar]]}} |
| − | {{Not selected tab|[[ | + | {{Not selected tab|[[1.3 Decimaltal|Nästa avsnitt >> ]]}} |
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
|} | |} | ||
| − | + | <!-- [[Media: Lektion 2 Rakneordning Ruta.pdf|<b><span style="color:blue">Lektion 2 Räkneordning</span></b>]] --> | |
| − | [[Media: Lektion 2 Rakneordning Ruta.pdf|< | + | |
| − | + | ||
| − | + | ||
| − | + | ||
== <b><span style="color:#931136">Hur räknar du?</span></b> == | == <b><span style="color:#931136">Hur räknar du?</span></b> == | ||
| − | <div class=" | + | <div class="ovnE"> |
[[Image: Hur raknar du 20a.jpg]] | [[Image: Hur raknar du 20a.jpg]] | ||
| − | + | <b><span style="color:red">Vanligt fel:</span></b> <math> \quad\;\;\, 6 \, + \, 3 \cdot 5 \, = \, 9 \cdot 5 \, = \, 45 </math> | |
| − | :<math> | + | <b>Rätt<span style="color:black">:</span></b> <math> \qquad\qquad 6 \, + \, 3 \cdot 5 \, = \, 6 \, + \, (3 \cdot 5) \, = \, 6 \, +\, 15 \, = \, 21 </math> |
| − | </div> <!-- | + | |
| + | </div> <!-- exempel --> | ||
<div class="tolv"> <!-- tolv1 --> | <div class="tolv"> <!-- tolv1 --> | ||
| − | + | Men varför är <math> \, 21 \, </math> rätt och <math> \, 45 \, </math> fel? Pga följande regel som är en överenskommelse mellan matematiker i hela världen: | |
| − | + | </div> <!-- tolv1 --> | |
| − | + | ||
| − | + | ||
| − | <div class="border- | + | <div class="border-divblue"><b>Multiplikation går före addition.</b></div> |
| + | <div class="tolv"> <!-- tolv1a --> | ||
| + | Denna regel används när båda räkneoperationerna <math> \, + \, </math> och <math> \, \cdot\;</math> är inblandade. | ||
| − | + | Operationen <math> \, \cdot\;</math> har högre prioritet än operationen <math> \, + \, </math> dvs <math> \, \cdot\;</math> måste alltid räknas före <math> \, + \, </math> varför <math> \, 3 \, </math> gånger <math> \, 5 \, </math> måste räknas först och <math> \, 6 \, + \, 15 \, </math> sedan. | |
Är denna regel något vi bara måste acceptera eller finns det någon logisk förklaring för den? För att besvara frågan måste vi fundera på vad vi egentligen gör när vi multiplicerar. | Är denna regel något vi bara måste acceptera eller finns det någon logisk förklaring för den? För att besvara frågan måste vi fundera på vad vi egentligen gör när vi multiplicerar. | ||
| Rad 42: | Rad 40: | ||
<div class="tolv"> <!-- tolv2 --> | <div class="tolv"> <!-- tolv2 --> | ||
| − | <math> {\color{Red} 3} \, \ | + | <b>Ex.:</b> <math> \qquad\qquad 6 \, + \, {\color{Red} 3} \cdot 5 \, = \, 6 \, + \, (3 \cdot 5) \, = \, 6 \, +\, 15 \, = \, 21 </math> |
| − | :: | + | <b>Varför?</b> <math> \qquad {\color{Red} 3} \, \cdot \, 5 \, </math> kan uppfattas som<span style="color:black">:</span> <math> \qquad {\color{Red} 3} \, \cdot \, 5 \; = \; \underbrace{5 \, + \, 5 \, + \, 5}_{{\color{Red} 3}\;\times} </math> |
| − | + | När vi sedan lägger till <math> \, 6 \, + \, </math> i början och ersätter <math> \, {\color{Red} 3} \cdot 5 \, </math> med <math> \, 5 \, + \, 5 \, + \, 5 \, </math> ser vi att <math> \, {\color{Red} 3} \, </math> inte längre finns med i räkneprocessen<span style="color:black">:</span> | |
| − | + | ||
| − | + | ||
:::<math> 6 \, + \quad {\color{Red} 3} \, \cdot \, 5 \; = \; 6 \, + \quad \underbrace{5 \, + \, 5 \, + \, 5}_{{\color{Red} 3}\;\times} \, = \, 6 \, +\, 15 \, = \, 21 </math> | :::<math> 6 \, + \quad {\color{Red} 3} \, \cdot \, 5 \; = \; 6 \, + \quad \underbrace{5 \, + \, 5 \, + \, 5}_{{\color{Red} 3}\;\times} \, = \, 6 \, +\, 15 \, = \, 21 </math> | ||
| − | + | Därför är det fel att addera <math> \, 6 \, </math> med <math> \, {\color{Red} 3} \, </math> när man ska beräkna <math> \; 6 \, + \, {\color{Red} 3} \cdot 5 \, </math>. | |
| − | + | <math>{\color{Red} 3} \, \cdot \, 5 \; </math> kan uppfattas som en förkortning för <b><span style="color:red">upprepad addition</span></b> av <math> \, 5 \, </math> med sig själv, <math> \, {\color{Red} 3} \, </math> gånger. | |
| − | + | <math> {\color{Red} 3} \, </math> är inget tal som ingår i beräkningen, utan endast en information om att <math> \, 5 \, </math> ska adderas <math> \, {\color{Red} 3} \, </math> gånger med sig själv. | |
| − | + | Vi förstår prioritetsregeln <math> \; \cdot \; </math> går före <math> \; + \; </math> bättre genom att tolka multiplikationen som en upprepad addition. | |
| − | + | Tanken kan vidareföras: Även <b><span style="color:red">division</span></b> kan tolkas som <b><span style="color:red">upprepad subtraktion</span></b>. När vi t.ex. räknar <math> 30 \, / \, 5 \, </math> kan vi skriva så här<span style="color:black">:</span> | |
:::::<math> 30 \; \underbrace{- \, 5 \, - \, 5 \, - \, 5 \, - 5 \, - 5 \, - \,5}_{{\color{Red} 6}\;\times} \; = \; 0 \qquad {\rm dvs} \qquad 30 \, / \, 5 \; = \; {\color{Red} 6}\,, \;\; {\rm rest\;\;} 0 </math> | :::::<math> 30 \; \underbrace{- \, 5 \, - \, 5 \, - \, 5 \, - 5 \, - 5 \, - \,5}_{{\color{Red} 6}\;\times} \; = \; 0 \qquad {\rm dvs} \qquad 30 \, / \, 5 \; = \; {\color{Red} 6}\,, \;\; {\rm rest\;\;} 0 </math> | ||
| − | Denna tolkning av division kommer även att hjälpa oss att förstå [[ | + | Denna tolkning av division kommer även att hjälpa oss att förstå [[Varför_är_division_med_0_inte_definierad%3F#Teoretisk_f.C3.B6rklaring|<b><span style="color:blue">varför man inte får dividera med 0</span></b>]]. |
</div> <!-- tolv2 --> | </div> <!-- tolv2 --> | ||
| Rad 72: | Rad 68: | ||
| − | <div class="border- | + | <div class="border-divblue">[[Image: De 4 raknesattens prioritetsregler 20.jpg]]</div> |
| Rad 90: | Rad 86: | ||
:::<math> 12 \, - \, 2 \cdot 3 \, + \, 6 </math> | :::<math> 12 \, - \, 2 \cdot 3 \, + \, 6 </math> | ||
| − | Som det sades inledningsvis är det vanligaste felet att börja räkna <math> \, 12 \, - \, 2 \, </math>. Istället för att börja räkna är det bättre att först titta på hela uttrycket. Då ser man att operatorerna <math> \, + \, </math> och <math> \, \cdot\;</math> är inblandade vilket innebär att prioritetsreglerna måste användas: | + | Som det sades inledningsvis är det vanligaste felet att börja räkna <math> \, 12 \, - \, 2 \, </math>. Istället för att börja räkna är det bättre att först titta på hela uttrycket. Då ser man att operatorerna <math> \, + \, </math> och <math> \, \cdot\;</math> är inblandade vilket innebär att prioritetsreglerna måste användas<span style="color:black">:</span> |
:::<math> 12 \, - \, 2 \cdot 3 \, + \, 6 \, = \, 12 \, - \, (2 \cdot 3) \, + \, 6 \, = \, 12 \, - \, 6 \, + \, 6 \, = \, 12</math> | :::<math> 12 \, - \, 2 \cdot 3 \, + \, 6 \, = \, 12 \, - \, (2 \cdot 3) \, + \, 6 \, = \, 12 \, - \, 6 \, + \, 6 \, = \, 12</math> | ||
| − | Parentesen är här endast till för att förtydliga hur man tänkt och räknat. Beakta uppgiftens redovisning som en < | + | Parentesen är här endast till för att förtydliga hur man tänkt och räknat. Beakta uppgiftens redovisning som en <b><span style="color:red">kedja av likheter</span></b> för att visa alla mellansteg. Likhetstecknets korrekta användning innebär att det verkligen står exakt samma sak på båda sidor av likhetstecknen. Därför måste t.ex. talet <math> \, 12 \, </math> upprepas i alla mellansteg ända till slutet för att upprätthålla likheterna, även om man inte räknar med <math> \, 12 \, </math> förrän i det allra sista steget. |
<!-- Genom skicklig användning av räkneordning kan man minimera räknearbetet. --> | <!-- Genom skicklig användning av räkneordning kan man minimera räknearbetet. --> | ||
</div> | </div> | ||
| Rad 102: | Rad 98: | ||
== <b><span style="color:#931136">Exempel 2</span></b> == | == <b><span style="color:#931136">Exempel 2</span></b> == | ||
| − | Här har vi ett lite större uttryck med parenteser: | + | Här har vi ett lite större uttryck med parenteser<span style="color:black">:</span> |
:::<math>(50+14)-8\cdot3+4</math> | :::<math>(50+14)-8\cdot3+4</math> | ||
| − | Om vi endast tillämpar det vi lärt oss i det här avsnittet dvs räknar först multiplikationen blir lösningen följande: | + | Om vi endast tillämpar det vi lärt oss i det här avsnittet dvs räknar först multiplikationen blir lösningen följande<span style="color:black">:</span> |
:::<math>(50+14)-8\cdot3+4 = (50+14)-24+4 = 64-24+4 = 40+4 = 44</math> | :::<math>(50+14)-8\cdot3+4 = (50+14)-24+4 = 64-24+4 = 40+4 = 44</math> | ||
| − | Men även följande lösning är helt korrekt: | + | Men även följande lösning är helt korrekt<span style="color:black">:</span> |
:::<math>(50+14)-8\cdot3+4 = 64-8\cdot3+4 = 64-24+4 = 40+4 = 44</math> | :::<math>(50+14)-8\cdot3+4 = 64-8\cdot3+4 = 64-24+4 = 40+4 = 44</math> | ||
| Rad 123: | Rad 119: | ||
== <b><span style="color:#931136">Exempel 3</span></b> == | == <b><span style="color:#931136">Exempel 3</span></b> == | ||
| − | '''Problem:''' Beräkna utan miniräknare: | + | '''Problem:''' Beräkna utan miniräknare<span style="color:black">:</span> |
:::<math>24 - (8-4) - 36/6 + 5\cdot4</math> | :::<math>24 - (8-4) - 36/6 + 5\cdot4</math> | ||
| Rad 138: | Rad 134: | ||
== <b><span style="color:#931136">Exempel 4</span></b> == | == <b><span style="color:#931136">Exempel 4</span></b> == | ||
| − | '''Problem:''' Beräkna utan räknare och kontrollera resultatet med räknaren: | + | '''Problem:''' Beräkna utan räknare och kontrollera resultatet med räknaren<span style="color:black">:</span> |
:::<math>\left({16-4 \over 3} + 7\right) \cdot 2 - 9/3 + 1 </math> | :::<math>\left({16-4 \over 3} + 7\right) \cdot 2 - 9/3 + 1 </math> | ||
| Rad 144: | Rad 140: | ||
'''Lösning:''' | '''Lösning:''' | ||
| − | :::<math> \displaystyle \left({16-4 \over 3} + 7\right)\,\cdot\,2\,-\,9/3\,+\,1 = \left({12 \over 3} + 7\right)\,\cdot\,2\,-\,3\,+\,1 = (4+7)\,\cdot\,2\,-\,3\,+\,1 = </math> | + | :::<math> \displaystyle \left({16-4 \over 3} + 7\right)\,\cdot\,2\,-\,9/3\,+\,1 = \left({12 \over 3} + 7\right)\,\cdot\,2\,-\,3\,+\,1 \, = (4+7)\,\cdot\,2\,-\,3\,+\,1 = </math> |
| − | :::<math> = 11\,\cdot\,2 | + | :::<math> = \, 11\,\cdot\,2\,-\,3\,+\,1 = 22\,-\,3\,+\,1 = 19\,+\,1 = 20 </math> |
Här har vi i det första mellansteget börjat att beräkna parentesen och samtidigt utfört divisionen <math>9/3</math> för att skriva lite mindre. Upplösningen av parentesen fortsätter i det andra mellansteget medan divisionen är avslutad och resultatet tas med i de följande mellanstegen tills parentesen är upplöst och multiplikationen med <math> \, 2 \, </math> genomförd. | Här har vi i det första mellansteget börjat att beräkna parentesen och samtidigt utfört divisionen <math>9/3</math> för att skriva lite mindre. Upplösningen av parentesen fortsätter i det andra mellansteget medan divisionen är avslutad och resultatet tas med i de följande mellanstegen tills parentesen är upplöst och multiplikationen med <math> \, 2 \, </math> genomförd. | ||
| Rad 152: | Rad 148: | ||
| − | == <b><span style="color:#931136"> | + | == <b><span style="color:#931136">Osynliga parenteser</span></b> == |
| − | <div class=" | + | <div class="ovnE"> |
| − | + | <table> | |
| + | <tr> | ||
| + | <td><big><b><span style="color:#931136">Exempel:</span></b></big> | ||
| − | + | </td> | |
| + | <td><math> \qquad\quad </math></td> | ||
| + | <td><math> \displaystyle{2+6 \over 3+1} </math></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <b><span style="color:red">Vanligt fel med digitalt verktyg:</span></b> <math> \quad 2 \, + \, 6 \, / \, 3 \, + \, 1 \, = \, 2 \, + \, 2 \, + \, 1 \, = \, 5 </math> | ||
| − | : | + | Rätt med digitalt verktyg<span style="color:black">:</span> <math> \qquad\qquad \color{Red}(2 + 6\color{Red}) / \color{Red}(3 + 1\color{Red}) \, = \, 8 \, / 4 \, = \, 2 </math> |
| − | + | Rätt med papper & penna<span style="color:black">:</span> <math> \displaystyle \qquad\quad\ {2+6 \over 3+1} = {(2+6) \over (3+1)} = {8 \over 4} = 2 </math> | |
| + | </div> | ||
| + | <div class="tolv"> <!-- tolv5 --> | ||
| + | Det finns två symboler för division som gör samma sak: Divisionstecknet som t.ex. i <math> \, \displaystyle {6/3} \, </math> och bråkstrecket som i <math> \, \displaystyle {6\over 3} \, </math>. | ||
| − | + | Skillnaden är att <math> \, \displaystyle {6/3} \, </math> är en <b><span style="color:red">operation</span></b>, nämligen att dividera <math> \, 6 \, </math> med <math> \, 3 \, </math>, medan <math> \, \displaystyle {6\over 3} \, </math> är ett <b><span style="color:red">tal</span></b> i bråkform. Båda ger <math> \, 2 </math>, operationens resultat och bråket förkortat. | |
| − | + | Förklaringen för felet i exemplet ovan är "osynliga" parenteser: En av de dolda egenskaperna hos bråkstrecket är nämligen att det grupperar sin täljare <math> \, 6+2 \, </math> och nämnare <math> \, 3+1 \, </math> i osynliga parenteser, dvs i sådana som kan utelämnas. I det rätta svaret på papper (ovan) har vi synliggjort de "osynliga" parenteserna. | |
| − | Det | + | Och då ser man att det är parenteserna som måste beräknas först. Det är inte fel att i bråkformen även skriva de osynliga parenteserna kring täljaren <math> \, 2 \, + \, 6 \, </math> och nämnaren <math>3+1</math>, men de är onödiga. Man brukar utelämna dem därför att bråkstrecket själv gör det redan tydligt att det är ''hela'' <math> \, 2 \, + \, 6 \, </math> som ska delas med ''hela'' <math> \, 3 \, + \, 1</math>. |
| − | :: | + | Vill man därmot skriva om divisionen med bråkstrecket till divisionen med divisionstecknet kan man göra det. Båda former är identiska<span style="color:black">:</span> |
| − | + | ::::<math> {2+6 \over 3+1} = (2+6) / (3+1) \, = \, 8 \, / 4 \, = \, 2 </math> | |
| − | + | I divisionsformen får man till skillnad från bråkformen inte utelämna parenteserna. Annars blir det ett annat uttryck och ett annat resultat<span style="color:black">:</span> | |
| − | + | ||
| + | ::::<math>2 \, + \, 6 \, / \, 3 \, + \, 1 \, = \, 2 \, + \, (6 \, / \, 3) \, + \, 1 \, = \, 2 \, + \, 2 \, + \, 1 \, = \, 5 </math> | ||
| − | + | Detta pga prioritetsregeln "Division går före addition". | |
| − | + | ||
| − | + | ||
| − | <div | + | '''Slutsats:''' |
| − | + | </div> <!-- tolv5 --> | |
| + | <div class="border-divblue"><b>Bråkstreck inkluderar parentes.</b></div> | ||
| − | |||
| − | + | == <b><span style="color:#931136">Parenteser och osynliga multiplikationstecken</span></b> == | |
| + | <div class="tolv"> <!-- tolv4 --> | ||
| + | Vad händer när parenteser är inblandade? Med parenteser kan man bryta prioritetsordningen och styra själv räknegången. | ||
| − | + | Om vi i det inledande exemplet sätter parenteser kan vi bryta prioritetsordningen och få <math> \, 45 \, </math><span style="color:black">:</span> | |
| − | + | ::::<math>(6+3)\cdot5=9\cdot5=45</math> | |
| − | + | ||
| − | + | Parentesen tvingar oss här att först räkna <math>6+3</math> och sedan fortsätta med gånger <math> \, 5 \, </math> så att man får <math> \, 45 \, </math>. Uttrycket ovan är ett annat uttryck än det inledande exemplet. För att få det inledande exemplet måste parenteserna sättas så här<span style="color:black">:</span> | |
| − | ::::<math> | + | ::::<math>6+(3\cdot5)=6+15=21</math> |
| − | + | Man kan också säga att det i det inledande exemplet fanns "osynliga" parenteser. Det är sådana som ''kan'' utelämnas utan att någon ändring sker. Nu har vi gjort dem synliga. De gör exakt samma sak som prioritetsregeln "multiplikation går före addition". Därför utelämnar man dem vanligtvis och låter prioritetsregeln göra jobbet. Men det är inte heller fel att skriva parenteserna för tydlighetens skull. | |
| − | + | Det finns inte bara osynliga parenteser utan även osynliga multiplikationstecken. De kan också utelämnas utan att någon ändring av uttryckets värde förekommer. I exemplet ovan kan man faktiskt utelämna multiplikationstecknet och skriva så här<span style="color:black">:</span> | |
| − | ::::<math> | + | ::::<math>(6+3)\;5</math> |
| − | + | Detta ger samma värde <math> \, 9 \, </math> gånger <math> \, 5 \, = \, 45 \, </math> som ovan. | |
| − | + | Självklart kan man inte alltid utelämna multiplikationstecknet, t.ex. inte mellan två rena siffror eller tal som ska multipliceras. Läsligheten får ju inte lida. I uttrycket <math> \, (6+3)\;5 \, </math> är det parentesen som gör att multiplikationstecknet kan utelämnas. | |
| − | + | </div> <!-- tolv4 --> | |
| − | + | ||
| − | </div> <!-- | + | |
== <b><span style="color:#931136">Sammanfattning</span></b> == | == <b><span style="color:#931136">Sammanfattning</span></b> == | ||
| − | <div class=" | + | <div class="border-divblue"> |
När både parenteser och operatorer är inblandade i ett räkneuttryck använd följande turordningsregler: | När både parenteser och operatorer är inblandade i ett räkneuttryck använd följande turordningsregler: | ||
| Rad 219: | Rad 222: | ||
3. Sist additioner och subtraktioner. | 3. Sist additioner och subtraktioner. | ||
| − | </div | + | </div> |
== <b><span style="color:#931136">Internetlänkar</span></b> == | == <b><span style="color:#931136">Internetlänkar</span></b> == | ||
| + | |||
| + | https://www.mathsisfun.com/operation-order-pemdas.html | ||
https://www.youtube.com/watch?v=lFxztfJ2bq4 | https://www.youtube.com/watch?v=lFxztfJ2bq4 | ||
| Rad 240: | Rad 245: | ||
| − | [[Matte:Copyrights|Copyright]] © | + | [[Matte:Copyrights|Copyright]] © 2021 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved. |
Nuvarande version från 4 januari 2021 kl. 09.55
| << Förra avsnitt | Genomgång | Övningar | Nästa avsnitt >> |
Hur räknar du?
Vanligt fel: \( \quad\;\;\, 6 \, + \, 3 \cdot 5 \, = \, 9 \cdot 5 \, = \, 45 \)
Rätt: \( \qquad\qquad 6 \, + \, 3 \cdot 5 \, = \, 6 \, + \, (3 \cdot 5) \, = \, 6 \, +\, 15 \, = \, 21 \)
Men varför är \( \, 21 \, \) rätt och \( \, 45 \, \) fel? Pga följande regel som är en överenskommelse mellan matematiker i hela världen:
Denna regel används när båda räkneoperationerna \( \, + \, \) och \( \, \cdot\;\) är inblandade.
Operationen \( \, \cdot\;\) har högre prioritet än operationen \( \, + \, \) dvs \( \, \cdot\;\) måste alltid räknas före \( \, + \, \) varför \( \, 3 \, \) gånger \( \, 5 \, \) måste räknas först och \( \, 6 \, + \, 15 \, \) sedan.
Är denna regel något vi bara måste acceptera eller finns det någon logisk förklaring för den? För att besvara frågan måste vi fundera på vad vi egentligen gör när vi multiplicerar.
Varför går multiplikation före addition?
Ex.: \( \qquad\qquad 6 \, + \, {\color{Red} 3} \cdot 5 \, = \, 6 \, + \, (3 \cdot 5) \, = \, 6 \, +\, 15 \, = \, 21 \)
Varför? \( \qquad {\color{Red} 3} \, \cdot \, 5 \, \) kan uppfattas som: \( \qquad {\color{Red} 3} \, \cdot \, 5 \; = \; \underbrace{5 \, + \, 5 \, + \, 5}_{{\color{Red} 3}\;\times} \)
När vi sedan lägger till \( \, 6 \, + \, \) i början och ersätter \( \, {\color{Red} 3} \cdot 5 \, \) med \( \, 5 \, + \, 5 \, + \, 5 \, \) ser vi att \( \, {\color{Red} 3} \, \) inte längre finns med i räkneprocessen:
- \[ 6 \, + \quad {\color{Red} 3} \, \cdot \, 5 \; = \; 6 \, + \quad \underbrace{5 \, + \, 5 \, + \, 5}_{{\color{Red} 3}\;\times} \, = \, 6 \, +\, 15 \, = \, 21 \]
Därför är det fel att addera \( \, 6 \, \) med \( \, {\color{Red} 3} \, \) när man ska beräkna \( \; 6 \, + \, {\color{Red} 3} \cdot 5 \, \).
\({\color{Red} 3} \, \cdot \, 5 \; \) kan uppfattas som en förkortning för upprepad addition av \( \, 5 \, \) med sig själv, \( \, {\color{Red} 3} \, \) gånger.
\( {\color{Red} 3} \, \) är inget tal som ingår i beräkningen, utan endast en information om att \( \, 5 \, \) ska adderas \( \, {\color{Red} 3} \, \) gånger med sig själv.
Vi förstår prioritetsregeln \( \; \cdot \; \) går före \( \; + \; \) bättre genom att tolka multiplikationen som en upprepad addition.
Tanken kan vidareföras: Även division kan tolkas som upprepad subtraktion. När vi t.ex. räknar \( 30 \, / \, 5 \, \) kan vi skriva så här:
- \[ 30 \; \underbrace{- \, 5 \, - \, 5 \, - \, 5 \, - 5 \, - 5 \, - \,5}_{{\color{Red} 6}\;\times} \; = \; 0 \qquad {\rm dvs} \qquad 30 \, / \, 5 \; = \; {\color{Red} 6}\,, \;\; {\rm rest\;\;} 0 \]
Denna tolkning av division kommer även att hjälpa oss att förstå varför man inte får dividera med 0.
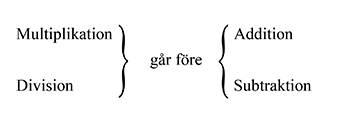
De fyra räknesättens prioritetsregler
Både multiplikation och division har alltså högre prioritet än addition och subtraktion.
Addition har samma prioritet som subtraktion.
Multiplikation har samma prioritet som division.
Exempel 1
Vad ger följande uttryck?
- \[ 12 \, - \, 2 \cdot 3 \, + \, 6 \]
Som det sades inledningsvis är det vanligaste felet att börja räkna \( \, 12 \, - \, 2 \, \). Istället för att börja räkna är det bättre att först titta på hela uttrycket. Då ser man att operatorerna \( \, + \, \) och \( \, \cdot\;\) är inblandade vilket innebär att prioritetsreglerna måste användas:
- \[ 12 \, - \, 2 \cdot 3 \, + \, 6 \, = \, 12 \, - \, (2 \cdot 3) \, + \, 6 \, = \, 12 \, - \, 6 \, + \, 6 \, = \, 12\]
Parentesen är här endast till för att förtydliga hur man tänkt och räknat. Beakta uppgiftens redovisning som en kedja av likheter för att visa alla mellansteg. Likhetstecknets korrekta användning innebär att det verkligen står exakt samma sak på båda sidor av likhetstecknen. Därför måste t.ex. talet \( \, 12 \, \) upprepas i alla mellansteg ända till slutet för att upprätthålla likheterna, även om man inte räknar med \( \, 12 \, \) förrän i det allra sista steget.
Exempel 2
Här har vi ett lite större uttryck med parenteser:
- \[(50+14)-8\cdot3+4\]
Om vi endast tillämpar det vi lärt oss i det här avsnittet dvs räknar först multiplikationen blir lösningen följande:
- \[(50+14)-8\cdot3+4 = (50+14)-24+4 = 64-24+4 = 40+4 = 44\]
Men även följande lösning är helt korrekt:
- \[(50+14)-8\cdot3+4 = 64-8\cdot3+4 = 64-24+4 = 40+4 = 44\]
Här har man löst upp parentesen först vilket inte alls står i motsägelse till prioritetsreglerna. Inom parentesen finns ju ingen annan operator än \( \, + \, \) så att det inte uppstår något problem vad gäller operatorprioritet. I nästa steg räknas \( \, 8 \, \) gånger \( \, 3 \, \) först och dras av sedan från \( \, 64 \, \). Viktigt är att man efter första likhetstecknet inte begår felet att räkna \(64-8\) utan tar först \( \, 8 \, \) gånger \( \, 3 \, \).
Frågan som uppstår nu är: Vilken av de två lösningarna ovan är bättre? Just i det här exemplet spelar det ingen roll. Men generellt kommer vi att se att det i större sammanhang är bättre att lösa upp parenteser först, dvs att räkna deras innehåll så att man kan ta bort dem. Sedan kan man följa operatorernas prioritetsregler.
Exempel 3
Problem: Beräkna utan miniräknare:
- \[24 - (8-4) - 36/6 + 5\cdot4\]
Lösning:
- \[24\,-\,(8-4)\,-\,36/6\,+\,5\,\cdot\,4\;=\;24\,-\,4\,-\,6\,+\,20\;=\;20\,-\,6\,+\,20\;=\;14\,+\,20\;=\;34\]
Här har vi förkortat lösningen genom att sammanfatta beräkningen av parentesen, divisionen och multiplikationen i det första mellansteget.
Exempel 4
Problem: Beräkna utan räknare och kontrollera resultatet med räknaren:
- \[\left({16-4 \over 3} + 7\right) \cdot 2 - 9/3 + 1 \]
Lösning:
- \[ \displaystyle \left({16-4 \over 3} + 7\right)\,\cdot\,2\,-\,9/3\,+\,1 = \left({12 \over 3} + 7\right)\,\cdot\,2\,-\,3\,+\,1 \, = (4+7)\,\cdot\,2\,-\,3\,+\,1 = \]
- \[ = \, 11\,\cdot\,2\,-\,3\,+\,1 = 22\,-\,3\,+\,1 = 19\,+\,1 = 20 \]
Här har vi i det första mellansteget börjat att beräkna parentesen och samtidigt utfört divisionen \(9/3\) för att skriva lite mindre. Upplösningen av parentesen fortsätter i det andra mellansteget medan divisionen är avslutad och resultatet tas med i de följande mellanstegen tills parentesen är upplöst och multiplikationen med \( \, 2 \, \) genomförd.
Osynliga parenteser
| Exempel: | \( \qquad\quad \) | \( \displaystyle{2+6 \over 3+1} \) |
Vanligt fel med digitalt verktyg: \( \quad 2 \, + \, 6 \, / \, 3 \, + \, 1 \, = \, 2 \, + \, 2 \, + \, 1 \, = \, 5 \)
Rätt med digitalt verktyg: \( \qquad\qquad \color{Red}(2 + 6\color{Red}) / \color{Red}(3 + 1\color{Red}) \, = \, 8 \, / 4 \, = \, 2 \)
Rätt med papper & penna: \( \displaystyle \qquad\quad\ {2+6 \over 3+1} = {(2+6) \over (3+1)} = {8 \over 4} = 2 \)
Det finns två symboler för division som gör samma sak: Divisionstecknet som t.ex. i \( \, \displaystyle {6/3} \, \) och bråkstrecket som i \( \, \displaystyle {6\over 3} \, \).
Skillnaden är att \( \, \displaystyle {6/3} \, \) är en operation, nämligen att dividera \( \, 6 \, \) med \( \, 3 \, \), medan \( \, \displaystyle {6\over 3} \, \) är ett tal i bråkform. Båda ger \( \, 2 \), operationens resultat och bråket förkortat.
Förklaringen för felet i exemplet ovan är "osynliga" parenteser: En av de dolda egenskaperna hos bråkstrecket är nämligen att det grupperar sin täljare \( \, 6+2 \, \) och nämnare \( \, 3+1 \, \) i osynliga parenteser, dvs i sådana som kan utelämnas. I det rätta svaret på papper (ovan) har vi synliggjort de "osynliga" parenteserna.
Och då ser man att det är parenteserna som måste beräknas först. Det är inte fel att i bråkformen även skriva de osynliga parenteserna kring täljaren \( \, 2 \, + \, 6 \, \) och nämnaren \(3+1\), men de är onödiga. Man brukar utelämna dem därför att bråkstrecket själv gör det redan tydligt att det är hela \( \, 2 \, + \, 6 \, \) som ska delas med hela \( \, 3 \, + \, 1\).
Vill man därmot skriva om divisionen med bråkstrecket till divisionen med divisionstecknet kan man göra det. Båda former är identiska:
- \[ {2+6 \over 3+1} = (2+6) / (3+1) \, = \, 8 \, / 4 \, = \, 2 \]
I divisionsformen får man till skillnad från bråkformen inte utelämna parenteserna. Annars blir det ett annat uttryck och ett annat resultat:
- \[2 \, + \, 6 \, / \, 3 \, + \, 1 \, = \, 2 \, + \, (6 \, / \, 3) \, + \, 1 \, = \, 2 \, + \, 2 \, + \, 1 \, = \, 5 \]
Detta pga prioritetsregeln "Division går före addition".
Slutsats:
Parenteser och osynliga multiplikationstecken
Vad händer när parenteser är inblandade? Med parenteser kan man bryta prioritetsordningen och styra själv räknegången.
Om vi i det inledande exemplet sätter parenteser kan vi bryta prioritetsordningen och få \( \, 45 \, \):
- \[(6+3)\cdot5=9\cdot5=45\]
Parentesen tvingar oss här att först räkna \(6+3\) och sedan fortsätta med gånger \( \, 5 \, \) så att man får \( \, 45 \, \). Uttrycket ovan är ett annat uttryck än det inledande exemplet. För att få det inledande exemplet måste parenteserna sättas så här:
- \[6+(3\cdot5)=6+15=21\]
Man kan också säga att det i det inledande exemplet fanns "osynliga" parenteser. Det är sådana som kan utelämnas utan att någon ändring sker. Nu har vi gjort dem synliga. De gör exakt samma sak som prioritetsregeln "multiplikation går före addition". Därför utelämnar man dem vanligtvis och låter prioritetsregeln göra jobbet. Men det är inte heller fel att skriva parenteserna för tydlighetens skull.
Det finns inte bara osynliga parenteser utan även osynliga multiplikationstecken. De kan också utelämnas utan att någon ändring av uttryckets värde förekommer. I exemplet ovan kan man faktiskt utelämna multiplikationstecknet och skriva så här:
- \[(6+3)\;5\]
Detta ger samma värde \( \, 9 \, \) gånger \( \, 5 \, = \, 45 \, \) som ovan.
Självklart kan man inte alltid utelämna multiplikationstecknet, t.ex. inte mellan två rena siffror eller tal som ska multipliceras. Läsligheten får ju inte lida. I uttrycket \( \, (6+3)\;5 \, \) är det parentesen som gör att multiplikationstecknet kan utelämnas.
Sammanfattning
När både parenteser och operatorer är inblandade i ett räkneuttryck använd följande turordningsregler:
1. Lös upp eventuella parenteser först, dvs räkna deras innehåll.
2. Sedan tar du multiplikationer och divisioner.
3. Sist additioner och subtraktioner.
Internetlänkar
https://www.mathsisfun.com/operation-order-pemdas.html
https://www.youtube.com/watch?v=lFxztfJ2bq4
http://matematikvideo.se/lektioner/prioriteringsreglerna/
http://www.matteguiden.se/rakneregler/
http://www.mathgoodies.com/lessons/vol7/order_operations.html
Copyright © 2021 TechPages AB. All Rights Reserved.