Skillnad mellan versioner av "3.3 Ekvationer+"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| (12 mellanliggande versioner av samma användare visas inte) | |||
| Rad 13: | Rad 13: | ||
| − | + | = <b><span style="color:#931136">Vad är en ekvation?</span></b> = | |
| − | + | ::[[Image: Ekvation Obekant VL HL_350.jpg]] | |
| − | + | ||
| − | + | ||
<br> | <br> | ||
<div class="border-divblue"> | <div class="border-divblue"> | ||
| Rad 49: | Rad 47: | ||
<b><span style="color:#931136">Kontroll</span></b> kallas ibland även för <b><span style="color:#931136">prövning.</span></b> | <b><span style="color:#931136">Kontroll</span></b> kallas ibland även för <b><span style="color:#931136">prövning.</span></b> | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Rad 101: | Rad 55: | ||
| − | + | = <b><span style="color:#931136">1. Övertäckningsmetoden</span></b> = | |
<br> | <br> | ||
| Rad 132: | Rad 86: | ||
| − | + | = <b><span style="color:#931136">2. Allmän metod</span></b> = | |
<br> | <br> | ||
| Rad 258: | Rad 212: | ||
</tr> | </tr> | ||
</table> | </table> | ||
| − | tioner och parenteser som till slut, när uttrycket beräknas, ger ett värde: <b><span style="color:red">uttryckets värde</span></b>, se | + | tioner och parenteser som till slut, när uttrycket beräknas, ger ett värde: <b><span style="color:red">uttryckets värde</span></b>, se 3.1 Algebraiska uttryck. |
---- | ---- | ||
<b><span style="color:red">Ekvation</span></b> är en likhet mellan två uttryck med endast EN obekant (än så länge i Matte 1). | <b><span style="color:red">Ekvation</span></b> är en likhet mellan två uttryck med endast EN obekant (än så länge i Matte 1). | ||
---- | ---- | ||
| − | <b><span style="color:red">Formel</span></b> är en likhet mellan två uttryck med minst två variabler, behandlas i | + | <b><span style="color:red">Formel</span></b> är en likhet mellan två uttryck med minst två variabler, behandlas i 3.7 Formler. |
</div> | </div> | ||
| Rad 273: | Rad 227: | ||
| − | [[Matte:Copyrights|Copyright]] © | + | [[Matte:Copyrights|Copyright]] © 2021 [https://www.techpages.se <b><span style="color:blue">TechPages AB</span></b>]. All Rights Reserved. |
Nuvarande version från 29 december 2020 kl. 19.59
| Genomgång | Quiz | Övningar | Genomgång+ |
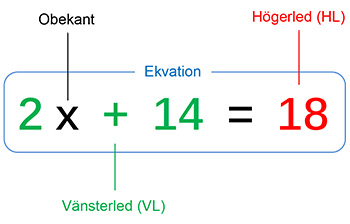
Vad är en ekvation?
En ekvation är en likhet mellan två uttryck,
har alltid formen VL = HL och innehåller i
regel en variabel, kallad obekant, t.ex. \( \, x \; \):
Ekvationen: \( \quad\;\; 2\,x \; + \; 14 \; = \; 18 \)
Lösningen: \( \qquad\qquad\;\; \)
- Varför lösning ?
Kontroll: Sätt in lösningen i ekvationen.
VL \( \, = \, 2 \, \cdot \, {\color{Red} 2} \, + \, 14 \, = \, 4 \, + \, 14 \, = \, 18 \)
HL \( \, = \, 18 \)
VL \( = \) HL \( \, \Rightarrow \, x = {\color{Red} 2} \) är en korrekt lösning.
Kontroll kallas ibland även för prövning.
Man säger: Lösningen satisfierar (uppfyller) ekvationen.
Två lösningsmetoder:
1. Övertäckningsmetoden
Exemplet ovan:
\( 2 \, x \;\; + \; 14 \; = \; 18 \quad {\color{Red} {\rm Täck\;över\;}} 2 \, x \)
\( \;\, {\color{Red} ?} \;\;\; + \; 14 \; = \; 18 \)
\( \;\, {\color{Red} 4} \;\;\; + \; 14 \; = \; 18 \)
\( \;\, \Downarrow \)
\( \, 2 \, \cdot \; x \;\; = \;\, {\color{Red} 4} \qquad\quad {\color{Red} {\rm Täck\;över\;}} x \)
\( \, 2 \, \cdot \; \)\( \, 2 \, \cdot \; {\color{Red} ?} \;\; = \;\; 4 \)
\( \, 2 \, \cdot \; {\color{Red} 2} \;\; = \;\; 4 \)
\( \quad\;\;\; \Downarrow \)
2. Allmän metod
Exempel:
- \[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & \qquad | & {\color{Red} {- \, 14}} \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} & & \\ 2 \cdot x \, & = & 4 & \qquad | & {\color{Red} {/ \; 2}} \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \\ x \, & = & 2 & & \end{array}\]
Skrivsättet \( \quad\;\;\, | \quad {\color{Red} {- \, 14}} \quad\;\;\, \) är en kommentar och betyder:
- Subtrahera \( \, 14 \, \) från ekvationens båda led.
Kommentaren \( \;\; | \quad {\color{Red} {/ \; 2}} \;\; \) betyder:
- Dividera ekvationens båda led med \( \, 2 \).
- Ekvation som en våg i balans
Målet: \( \qquad\quad \) Att isolera \( \, {\color{Red} x} \, \) på ett led.
Steg 1:
Förenkla uttrycken i ekvationens båda led så långt som
möjligt. I exemplet ovan:
- \[\begin{array}{rclcl} x \, + \, (x \, + \, 14) & = & 18 & & \\ x \, + \, x \, + \, 14 & = & 18 & & \\ 2\,x \, + \, 14 & = & 18 & & \end{array}\]
Steg 2:
Utför samma operation på ekvationens båda led:
- \[\begin{array}{rcl} 2\,x \, + \, 14 & = & 18 \qquad\quad | \;\; {\color{Red} {- \, 14}} \\ 2\,x \, + \, 14 \, {\color{Red} {- \, 14}} & = & 18 \, {\color{Red} {- \, 14}} \\ \end{array}\]
Förenkla de nyuppkomna uttrycken.
- \[\begin{array}{rclcl} \quad\; 2 \cdot x \, & = & 4 & \qquad | & {\color{Red} {/ \; 2}} \\ \displaystyle \frac{2 \cdot x}{{\color{Red} {2}}} & = & \displaystyle \frac{4}{{\color{Red} {2}}} & & \end{array}\]
Förenkla de nyuppkomna uttrycken:
- \[\begin{array}{rclcl} \quad\; x \, & = & 2 & & \end{array}\]
\( \qquad\quad \) Vilken operation?
Regel: Den inversa operationen med målet att isolera \( \, x \, \).
- \[ 2\,x \, + \, 14 \; = \; 18 \qquad\quad | \;\; {\color{Red} {- \, 14}} \]
Eftersom:
\( \, {\color{Red} {- \, 14}} \, \) är den inversa (motsatta) operationen till \( \, + \, 14 \, \).
- \[ \;\; 2 \cdot x \; = \; 4 \qquad\quad\;\;\, | \;\; {\color{Red} {/ \; 2}} \]
Eftersom:
\( \, {\color{Red} {/ \; 2}} \, \) är den inversa operationen till \( \, \cdot \; 2 \, \).
Begreppsförklaringar
bokstäver, jämförbart med lådor som har etiketter. Innehållet är variabelns värde (tal) och kan bytas ut. Obekant är en variabel som förekommer i en ekvation. Uttryck är en kombination av variabler, tal, räkneopera- |
God redovisningsstil vid ekvationslösning:
|
tioner och parenteser som till slut, när uttrycket beräknas, ger ett värde: uttryckets värde, se 3.1 Algebraiska uttryck.
Ekvation är en likhet mellan två uttryck med endast EN obekant (än så länge i Matte 1).
Formel är en likhet mellan två uttryck med minst två variabler, behandlas i 3.7 Formler.
Copyright © 2021 TechPages AB. All Rights Reserved.