Skillnad mellan versioner av "3.3 Terasspunkter"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 41: | Rad 41: | ||
<math> f\,'(a) \, = \, f\,''(a) \, = \, 0 \; </math> och <math> \; f\,'''(a) \, \neq \, 0 \quad \Longrightarrow \quad </math> Funktionen <math> \; y = f(x) \; </math> har en <strong><span style="color:red">terasspunkt</span></strong> i <math> \; x = a \; </math>. | <math> f\,'(a) \, = \, f\,''(a) \, = \, 0 \; </math> och <math> \; f\,'''(a) \, \neq \, 0 \quad \Longrightarrow \quad </math> Funktionen <math> \; y = f(x) \; </math> har en <strong><span style="color:red">terasspunkt</span></strong> i <math> \; x = a \; </math>. | ||
---- | ---- | ||
| − | Om <math> \ | + | Om <math> \, f\,'(a) = f\,''(a) = f\,'''(a) = 0 \, </math> kan endast en korrekt [[3.2_Lokala_maxima_och_minima#Regler_om_max.2Fmin_med_teckenstudie|<b><span style="color:blue">teckenstudie</span></b>]] avgöra den kritiska punktens typ, se nedan. |
</div> | </div> | ||
| − | |||
| − | |||
Tredjederivatan är inget annat än andraderivatans derivata. Man får den genom att derivera andraderivatan en gång till enligt deriveringsreglerna. | Tredjederivatan är inget annat än andraderivatans derivata. Man får den genom att derivera andraderivatan en gång till enligt deriveringsreglerna. | ||
| − | |||
| − | |||
==== <b><span style="color:#931136">Kritiska punkter</span></b> ==== | ==== <b><span style="color:#931136">Kritiska punkter</span></b> ==== | ||
Versionen från 23 februari 2016 kl. 20.14
| <-- Förra avsnitt | Genomgång | Övningar | --> Nästa avsnitt |
Även i detta avsnitt antar vi att alla behandlade funktioner \( \; y \, = \, f(x) \; \) skall vara kontinuerliga i alla punkter av det betraktade området.
Vad är en terasspunkt?
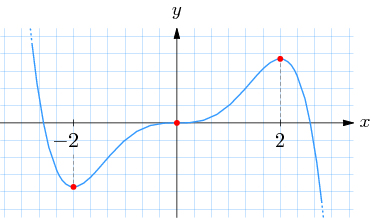 |
Bilden till vänster visar tre punkter där kurvan har tangenter med lutningen \( \, 0 \):
|
Regeln om terasspunkt med derivator
\( f\,'(a) \, = \, f\,''(a) \, = \, 0 \; \) och \( \; f\,'''(a) \, \neq \, 0 \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har en terasspunkt i \( \; x = a \; \).
Om \( \, f\,'(a) = f\,''(a) = f\,'''(a) = 0 \, \) kan endast en korrekt teckenstudie avgöra den kritiska punktens typ, se nedan.
Tredjederivatan är inget annat än andraderivatans derivata. Man får den genom att derivera andraderivatan en gång till enligt deriveringsreglerna.
Kritiska punkter
En punkt \( \, x = a \, \) kallas för kritisk punkt om \( \, f\,'(a) = 0 \, \).
En kritisk punkt kan vara ett maximum, ett minimum eller en terasspunkt.
Ett annat namn för kritiska punkter är stationära punkter. Stationära, därför att kurvan "stannar av" i dessa punkter, dvs lutningen är \( \, 0\): Kurvan är varken växande eller avtagande.
Exempel på terasspunkt med derivator
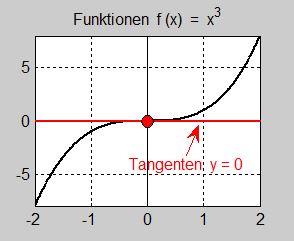
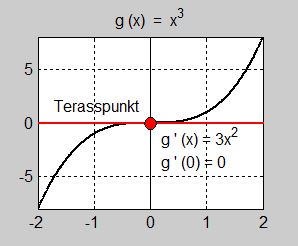
Undersök med derivator vilken typ av kritisk punkt funktionen \( \, f(x) = x\,^3 \, \) har i punkten \( \, x = 0 \, \).
Lösning med derivator:
- \[\begin{array}{rclclcl} f(x) & = & x\,^3 & & \\ f'(x) & = & 3\,x\,^2 & \Longrightarrow & f'(0) = 3\cdot 0^2 = 3\cdot 0 & = & 0 \\ f''(x) & = & 6\,x & \Longrightarrow & f''(0) = 6\cdot 0 & = & 0 \\ f'''(x) & = & 6 & \Longrightarrow & f'''(0) = 6 & \neq & 0 \end{array}\]
Vi ser att \( \, f\,'(0) = f\,''(0) = 0 \, \) och \( \, f\,'''(0) \neq 0 \). Av regeln ovan följer att \( \, f(x)\, \) har en terasspunkt i \( \, x = 0 \, \) som visas på bilden till vänster.
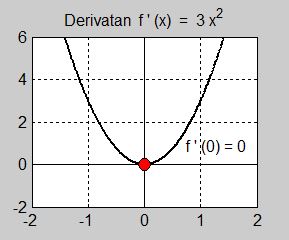
Bilden i mitten visar att derivatan har ett nollställe i \( \, x = 0 \, \). Det speciella med detta nollställe är att kurvan inte skär \( \, x\)-axeln utan endast berör den. Med andra ord, \( \, x = 0 \, \) är en dubbelrot till andragradsfunktionen \( \, f\,'(x) = 3\,x^2 \, \). Detta innebär att derivatan inte byter tecken kring \( \, x = 0 \, \) dvs är positiv både till vänster och till höger om nollstället. Att derivatan är positiv på båda sidor av sitt nollställe innebär i sin tur att själva funktionen \( \, f(x) = x^3 \, \) är växande både till vänster om och till höger om \( \, x = 0 \, \) \(-\) vilket är ett kännetecken för terasspunkter. En annan konsekvens av derivatans dubbelrot är att andraderivatan är \( \, 0 \, \) i \( \, x = 0 \, \):
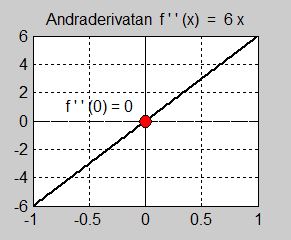
Bilden till höger visar att även andraderivatan är \( \, 0 \, \) i \( \, x = 0 \, \). Till skillnad från derivatans nollställe är detta nollställe av enkel typ, vilket framgår av att grafen verkligen skär \( \, x\)-axeln dvs byter tecken kring \( \, x = 0 \, \). I självaste punkten \( \, x = 0 \, \) är andraderivatan varken positiv eller negativ, varav följer att \( \, x = 0 \, \) inte är någon extrempunkt för funktionen \( \, f(x) = x^3 -\) ytterliare ett kännetecken för terasspunkter. En annan konsekvens av att andraderivatans rot är av enkel typ är att tredjederivatan är \( \, \neq 0 \, \) i \( \, x = 0 \, \).
Alternativt till användning av derivator finns det alltid möjligheten att genomföra en teckenstudie för att känna igen en terasspunkt:
Regeln om terasspunkt med teckenstudie
\( f\,'(a) = 0 \; \) och \( \; f\,'(x) \) inte byter tecken kring \( \, x=a \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har en terasspunkt i \( \; x = a \; \).
Med andra ord, i en terasspunkt \( \, x=a \) måste derivatan vara \( \, 0 \), utan att byta tecken kring \( \, a \), dvs derivatan är antingen positiv eller negativ på båda sidor av \( \, x=a \).
Exempel på terasspunkt med teckenstudie
Undersök med en teckenstudie vilken typ av kritisk punkt funktionen \( \, f(x) = x\,^3 \, \) har i punkten \( \, x = 0 \, \).
Lösning med teckenstudie:
| Vi hade redan bestämt att
derivatan var \( \, 0 \) för \( \, x = 0 \, \):
|
|
Nu ska vi undersöka derivatans tecken till vänster och till höger om nollstället \( \, x = 0 \).
Vi väljer t.ex. punkterna \( \, x = -0,1 \) och \( \, x = 0,1 \) och bestämmer derivatans tecken i dessa punkter:
|
|
Dessa resultat är infogade i teckentabellen till höger som visar:
- \( \, f\,'(0) = 0 \, \)
- Derivatan har tecknet \(+\) till vänster och även \( + \) till höger om \( \, 0 \, \) dvs derivatan byter inte tecken kring sitt nollställe.
Enligt regeln om terasspunkt med teckenstudie drar vi slutsatsen att funktionen \( f(x)\, \) har en terasspunkt i \( \, x = 0 \).
Avgörande för att teckenstudie är en korrekt algebraisk metod är förutsättningen vi gjorde inledningsvis, nämligen att \( \; y \, = \, f(x) \; \) är kontinuerlig i alla punkter av det betraktade området.
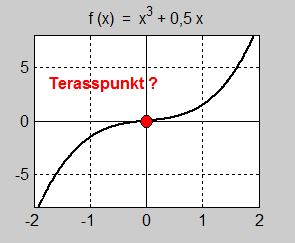
Hur grafen kan lura oss
- \[\begin{array}{rcl} f(x) & = & x^3 + \, 0,5\,x \\ f'(x) & = & 3\,x^2 + \, 0,5 \\ f'(0) & = & 3\cdot 0^2 + \, 0,5 = 3\cdot 0 \, + \, 0,5 = 0 \, + \, 0,5 \, = \, 0,5 \, \neq \, 0 \end{array}\]
Dvs redan första kravet i regeln om terasspunkt med derivator, nämligen att derivatan ska vara \( \, 0 \, \) för \( \, x = 0 \, \) är inte uppfyllt: \( \, f(x) \, \) har ingen terasspunkt i \( \, x = 0 \, \). Grafen har lurat oss.
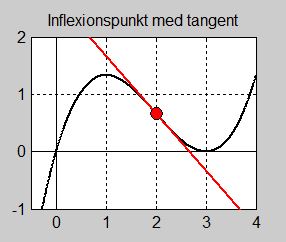
Vill man använda grafer borde man först undersöka funktionen med de strikta algebraiska reglerna och sedan rita grafer för att visualisera resultatet. I det här fallet är det lämpligt att även rita tangenten till \( \, f(x) \, \) i \( \, x = 0 \, \). Lägger man till graferna till derivatan och andraderivatan får man en fullständig överblick över funktionens beteende i och kring \( \, x = 0 \, \):
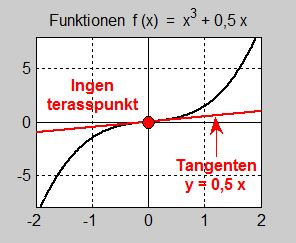
Bilden till vänster visar funktionens graf samt tangenten till kurvan i \( \, x = 0 \). Tangenten är inte horisontell dvs har inte lutningen \( \, 0 \). I beräkningen ovan hade vi fått: \( f'(x) = 0,5 \neq 0 \). Därmed är även tangentens lutning \( \, 0,5 \, \) och dess ekvation: \( y = 0,5\,x \). Därför föreligger i \( \, x = 0 \, \) inte en terasspunkt.
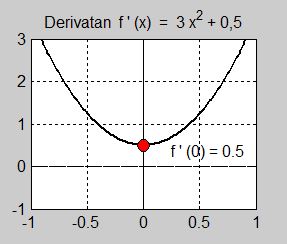
Bilden i mitten visar att derivatan inte har något nollställe vilket visar att funktionen varken har extrempunkter eller terasspunkter. Derivatan är alltid positiv och antar i \( x = 0 \) värdet \( \, 0,5 \, \). Om detta värde hade varit \( \, 0 \, \) hade funktionen haft en terasspunkt i \( x = 0 \).
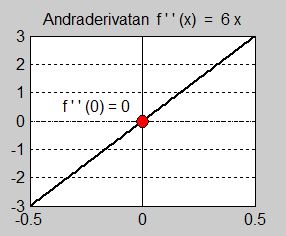
Bilden till höger visar att andraderivatan har ett nollställe i \( \, x = 0 \, \), där grafen skär \( \, x\)-axeln. Vad innebär detta? Vi har inte haft ett sådant fall där derivatan är skild från \( \, 0 \, \), men andraderivatan är \( \, 0 \, \). Därför handlar det om en speciell punkt på kurvan som varken är extrem- eller terasspunkt, för i dessa fall borde ju derivatan vara \( \, 0 \, \). Faktiskt handlar det om en ny typ av punkt som kallas inflexionspunkt.
Inflexionspunkter
Terasspunkter är specialfall av inflexionspunkter, eftersom kurvan byter alltid svängriktning i en terasspunkt.
Men inte alla inflexionspunkter är terasspunkter. Inflexionspunkter kan ha tangenter med vilken lutning som helst.
Terasspunkter är sådana inflexionspunkter där tangenten har lutningen \( \, 0 \, \).
Pga funktionens kontinuitet finns alltid en inflexionspunkt mellan två extrempunkter.
Regeln om inflexionspunkter
\( f\,''(a) \, = \, 0 \; \) och \( \; f\,'''(a) \, \neq \, 0 \; \quad \Longrightarrow \quad \) Funktionen \( \; y \, = \, f(x) \; \) har en inflexionspunkt i \( \; x = a \; \).
Om dessutom \( \; f\,'(a) \, = \, 0 \; \) är \( \; x = a \; \) en terasspunkt. (Samma som tidigare)
En terasspunkt är alltid en inflexionspunkt, men inte tvärtom.
För att hitta inflexionspunkter ställer man alltså upp andraderivatan, sätter den till \( \, 0 \, \) och beräknar\( \, x \), dvs andraderivatans nollställen. Sedan kontrollerar man om tredjederivatan verkligen är skild från \( \, 0 \, \) för andraderivatans nollställen.
Dessutom gäller det: Om \( \, f\,'''(a) > 0 \, \) är kurvan konkav i \( \, x = a \ ,\) och vi har en övergång från höger- till vänstersväng \(-\) som i grafen ovan. Om däremot \( \, f\,'''(a) < 0 \, \) är kurvan konvex i \( \, x = a \ ,\) och kurvan går över från en vänster- till en högersväng.
Copyright © 2011-2016 Math Online Sweden AB. All Rights Reserved.