Skillnad mellan versioner av "3.2 Lokala maxima och minima"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 3: | Rad 3: | ||
{{Not selected tab|[[2.2 Genomsnittlig förändringshastighet|<-- Förra demoavsnitt]]}} | {{Not selected tab|[[2.2 Genomsnittlig förändringshastighet|<-- Förra demoavsnitt]]}} | ||
{{Selected tab|[[3.2 Lokala maxima och minima|Genomgång]]}} | {{Selected tab|[[3.2 Lokala maxima och minima|Genomgång]]}} | ||
| − | {{Not selected tab|[[ | + | {{Not selected tab|[[Dessa övningar ingår inte i demon.|Övningar]]}} |
{{Not selected tab|[[3.5 Extremvärdesproblem|--> Nästa demoavsnitt]]}} | {{Not selected tab|[[3.5 Extremvärdesproblem|--> Nästa demoavsnitt]]}} | ||
| style="border-bottom:1px solid #797979" width="100%"| | | style="border-bottom:1px solid #797979" width="100%"| | ||
Versionen från 14 februari 2016 kl. 00.48
| <-- Förra demoavsnitt | Genomgång | Övningar | --> Nästa demoavsnitt |
Lektion 30 Lokala maxima och minima I
Lektion 31 Lokala maxima och minima II
Det förutsätts att alla funktioner \( \; y \, = \, f(x) \; \) vi behandlar här är kontinuerliga i alla punkter av det betraktade området.
Andraderivata
Med andraderivata menas derivatans derivata som betecknas med \( \, f\,''(x) \, \) och läses \( \; {\rm "}\!f \; {\rm biss\;av\; } x\,{\rm"} \, \).
Man får andraderivatan genom att derivera derivatans funktion en gång till enligt deriveringsreglerna.
Regler om max/min med andraderivatan
\( f\,'(a) \, = \, 0 \; \) och \( \; f\,''(a) \, {\bf {\color{Red} <}} \, 0 \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har ett maximum i \( \; x = a \; \).
\( f\,'(a) \, = \, 0 \; \) och \( \; f\,''(a) \, {\bf {\color{Red} >}} \, 0 \quad \Longrightarrow \quad \) Funktionen \( \; y = f(x) \; \) har ett minimum i \( \; x = a \; \).
Med andra ord, det är derivatans nollställen och andraderivatans tecken i derivatans nollställen som avgör om en funktion har maxima eller minima.
Förklaring:
Om både \( \, f\,'(a) = 0 \, \) och \( \, f\,''(a) = 0 \, \) måste ytterligare undersökningar göras, vilket behandlas i nästa avsnitt.
Exempel 1 Vinternattens kallaste tidpunkt
Lösning med andraderivatan:
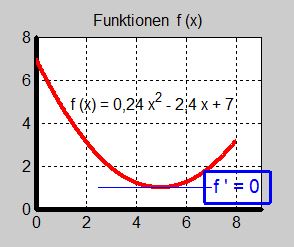
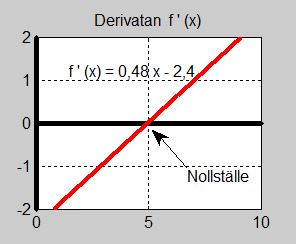
a) \( f(x) \, = \, 0,24\,x^2 - 2,4\,x + 7 \qquad\qquad\qquad\quad\;\; f\,'(x) \, = \, 0,48\,x - 2,4 \qquad\qquad\qquad\qquad\quad\; f\,''(x) \, = \, 0,48 \)
b) Reglerna om max/min med andraderivatan kräver derivatans nollställen. Därför sätter vi derivatan till \( \, 0 \, \) och beräknar \( \, x \):
- \[\begin{array}{rcrcl} f'(x) & = & 0,48\,x - 2,4 & = & 0 \\ & & 0,48\,x & = & 2,4 \\ & & x & = & {2,4 \over 0,48} \\ & & x & = & 5 \end{array}\]
Derivatan blir \( \, 0 \, \) för \( \, x = 5 \): Tangenten till kurvan \( \, y = f(x) \, \) har lutningen \( \, 0\, \) dvs är horisontell i \( \, x = 5 \, \).
Av detta följer att \( \, x = 5 \, \) är en extrempunkt. Men en extrempunkt kan vara ett maximum eller ett minimum.
För att avgöra om denna extrempunkt är ett maximum eller ett minimum kräver regeln andraderivatans tecken.
Därför sätter vi \( \, x = 5 \, \) in i andraderivatan och kollar om den blir positiv eller negativ:
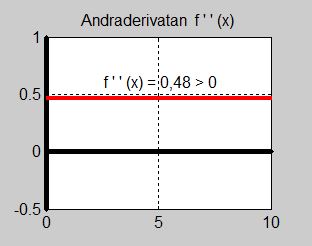
- \[ f\,''(x) \, = \, 0,48 \]
- \[ f\,''(5) = 0,48 \,>\, 0 \]
Andraderivatan är positiv (konstant) för alla \( x \, \) och därmed även för \( x = 5 \, \). Därav följer att \( \, f(x) \, \) har ett minimum i \( \; \boxed{x_{min} \, = \, 5} \; \).
Alltså är nattens kallaste tidpunkt kl \( \, 5 \, \).
c) Temperaturen vid kl \( \, 5 \, \) är:
- \[ f(x_{min}) = f(5) = 0,24 \cdot 5^2 - 2,4 \cdot 5 + 7 = 1 \]
Alltså är nattens lägsta temperatur \( \, 1 \, \) grad Celsius.
En alternativ metod för att skilja mellan max och min är teckenstudium som till skillnad från metoden med andraderivatan klarar sig med endast första derivatan:
Regler om max/min med teckenstudium
\( f\,'(a) \, = \, 0 \; \) och \( \; f\,'(x) \; \) byter tecken från \( \, + \, \) till \( \, - \, \) kring \( \, a \quad \Longrightarrow \quad y = f(x) \, \) har ett maximum i \( \, x = a \, \).
\( f\,'(a) \, = \, 0 \; \) och \( \; f\,'(x) \; \) byter tecken från \( \, - \, \) till \( \, + \, \) kring \( \, a \quad \Longrightarrow \quad y = f(x) \, \) har ett minimum i \( \, x = a \, \).
Med andra ord, det är derivatans nollställen och derivatans teckenbyte kring derivatans nollställen som avgör om en funktion har maxima eller minima.
Förklaring:
Om derivatan \( \, f\,'(a) = 0 \, \) men \( \, f\,'(x) \, \) inte byter tecken kring \( \, a \) måste ytterligare undersökningar göras, vilket behandlas i nästa avsnitt.
För att demonstrera regeln ovan tar vi samma Exempel 1 Vinternattens kallaste tidpunkt som behandlades tidigare. Vi bibehåller frågeställningen, men byter lösningsmetod:
Exempel 1 Vinternattens kallaste tidpunkt med teckenstudium
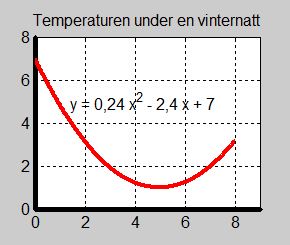
Under en vinternatt varierar temperaturen enligt funktionen
- \[ y \, = \, f(x) \, = \, 0,24\,x^2\,-\,2,4\,x\,+\,7 \]
där \( y \;\, = \) temperaturen i grader Celsius och
\( x \;\, = \) tiden i timmar efter midnatt
Funktionen \(\, f(x)\):s definitionsmängd: \( \quad 0 \leq x \leq 8 \)
Bestäm nattens kallaste tidpunkt med teckenstudium.
Lösning med teckenstudium:
Vi bestämmer fortfarande derivatans nollställen, men använder teckenstudium för att skilja mellan max/min.
Derivatans nollställe \( \, x = 5 \, \) tar vi över från Lösning med andraderivatan och bekräftar:
- \[ f(x) = 0,24\,x^2 - 2,4\,x + 7 \]
- \[ f'(x) = 0,48\,x - 2,4 \]
- \[ f' (5) = 0,48\cdot 5 - 2,4 = 0 \]
För att avgöra om \( \, x = 5 \, \) är maximi- eller minimipunkt måste vi undersöka derivatans tecken till vänster och till höger om denna punkt.
Vi väljer t.ex. punkterna \( \, x = 4,9 \, \) och \( \, x = 5,1 \, \) på \( \, x\)-axeln och bestämmer derivatans tecken i dessa punkter:
|
|
Dessa resultat är infogade i teckentabellen till höger och visar att \( \, f(x)\, \) antar ett minimum i \( \; \boxed{x_{min} \, = \, 5} \; \),
därför att \( \, f\,'(5) = 0 \) och derivatan byter tecken från \(-\) till \( + \) kring \( \, 5 -\) allt enligt reglerna ovan.
Därför inträffar nattens kallaste tidpunkt kl \( \, 5 \).
Sammanfattning:
Gemensamt för alla maxima och minima är att derivatan där är \( \, 0 \), därför att tangenten har lutningen \( \, 0 \, \). Följaktligen:
Genom att bilda derivatan, sätta den till \( \, 0 \, \) och beräkna \( \, x \), får vi reda på maximi- och minimipunkternas \( \, x\)-koordinater.
Sedan gäller det att skilja mellan maximi- och minimipunkter antingen med andraderivatan: eller Teckenstudium:.
Exempel 2 Maximal företagsvinst
Vi återgår till Exempel 3 i förra avsnitt, men byter frågeställning:
Efter statistiska observationer har man kommit fram till att ett företags vinst kan beräknas enligt funktionen:
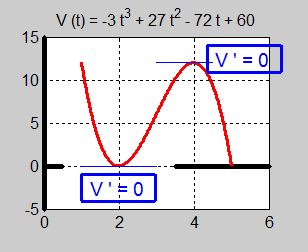
- \[ V(t) \; = \; -3\,t^3\,+\,27\,t^2\,-\,72\,t\,+\,60 \]
där \( V \; = \) företagets vinst i \( 1\,000 \) kr och
\( t \;\, = \) tiden i antalet år efter årsskiftet 2009/2010 \(. \qquad \) Definitionsområde: \( \; 1 \leq t \leq 5 \)
a) Ställ upp första- och andraderivatan. Rita graferna till \( \,V(t) \), \( \,V\,'(t) \) och \( \,V\,''(t) \) i separata koordinatsystem.
b) När har företaget maximal vinst? Denna uppgift ska lösas både med andraderivatan och teckentabellen.
c) Hur stor är företagets maximala vinst?
Frågorna b) och c) ska besvaras algebraiskt.
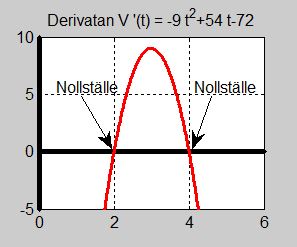
b) Derivatan är en 2:a gradsfunktion och har två reella nollställen. För att få reda på dem sätter vi derivatan till \( \, 0 \):
- \[\begin{array}{rcrcl} V'(t) & = & -9\,t^2 + 54\,t - 72 & = & 0 \\ & & t^2 - 6 \,t + 8 & = & 0 \end{array}\]
- 2:a gradsekvationen kan enkelt och snabbt lösas med Vieta:
- \[ \begin{array}{rcl} t_1 \cdot t_2 & = & 8 \\ t_1 + t_2 & = & -(-6) = 6 \\ &\Downarrow& \\ t_1 & = & 2 \\ t_2 & = & 4 \end{array}\]
- Dvs \( V'(2) = V'(4) = 0\, \) vilket innebär:
- Tangenterna till kurvan \( V(t)\, \) i punkterna \( t_1 = 2 \, \) och \( t_2 = 4 \, \) har lutningen \( 0\, \) dvs är horisontella.
- Horisontella tangenter kan innebära att kurvan har maximum eller minimum i dessa punkter.
- För att skilja mellan max och min använder vi två metoder: andraderivatan och teckentabellen \(-\) en i taget:
b) forts. med andraderivatan:
- Reglerna om max/min med andraderivatan tillämpas på derivatans båda nollställen.
- Nollställe 1: \( \; t_1 = 2 \quad \; \)
- Vi sätter in \( t_1 = 2 \, \) i andraderivatan och kollar om den blir positiv eller negativ:
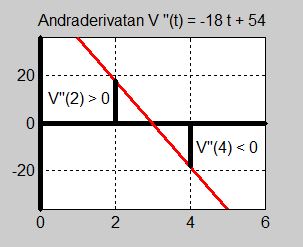
- \[ V\,''(t) \, = \, -18\,t + 54 \]
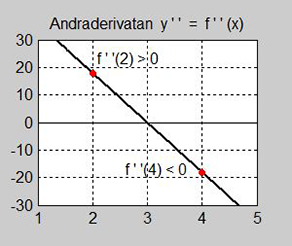
- \[ V\,''(2) \, = \, -18\cdot 2 + 54 = 18 > 0 \]
- Andraderivatan är positiv för \( t_1 = 2 \, \). Slutsats: \( V(t) \, \) har ett minimum i \( t_1 = 2 \, \).
- Nollställe 2: \( \; t_2 = 4 \quad \; \)
- Vi sätter in \( t_2 = 4 \, \) in i andraderivatan och kollar om den blir positiv eller negativ:
- \[ V\,''(4) \, = \, -18\cdot 4 + 54 = -18 < 0 \]
- Andraderivatan är negativ för \( t_2 = 4 \, \). Slutsats: \( V(t) \, \) har ett maximum i \( t_2 = 4 \, \).
- Alltså har företaget sin största vinst efter \( t_2 = 4 \, \) år efter årsskiftet 2009/2010, dvs vid årsskiftet 2013/2014.
b) forts. med teckenstudium:
- Reglerna om max/min med teckenstudium tittar på derivatans teckenbyte i en nära omgivning av derivatans nollställen.
- Vi tillämpar regeln enskilt på vart och ett nollställe.
- Nollställe 1: \( \; t_1 = 2 \)
- Vi väljer t.ex. punkterna \( \, t = 1,9 \) och \( \, t = 2,1 \) på t-axeln och bestämmer derivatans tecken i dessa punkter:
- \[ V'(t) = -9\,t^2 + 54\,t - 72 \]
- \[ V' (1,9) = -9\cdot 1,9^2 + 54\cdot 1,9 - 72 = -1,89 < 0 \]
- \[ V' (2,1) = -9\cdot 2,1^2 + 54\cdot 2,1 - 72 = 1,71 > 0 \]
- Nollställe 2: \( \; t_2 = 4 \)
- Vi väljer t.ex. punkterna \( \, t = 3,9 \) och \( \, t = 4,1 \) på t-axeln nära \( t_2 \) och bestämmer derivatans tecken i dessa punkter:
|
|
- Resultaten från båda nollställena skrivs in i teckentabellen ovan till höger som slutligen kan förenklas till följande teckentabell:
| \(t\) | \(2\) | \(4\) | |||
| \( V\,'(t) \) | \(-\) | \(0\) | \(+\) | \(0\) | \(-\) |
| \( \,V(t) \) | ↘ | Min | ↗ | Max | ↘ |
- Slutsatser:
- \( V(t)\, \) har ett minimum i \( \, t_1 = 2 \), därför att \( V\,'(2) = 0 \) och \( V\,'(t) \) byter tecken från \(-\) till \( + \) kring \( \, 2 \).
- \( V(t)\, \) har ett maximum i \( \, t_2 = 4 \), därför att \( V\,'(4) = 0 \) och \( V\,'(t) \) byter tecken från \(+\) till \( - \) kring \( \, 4 \).
- Resultatet är förstås det samma som i b) forts. med andraderivatan:
- Företaget har sin största vinst efter \( \, t_2 \, = \, t_{max} \, = \, 4 \, \) år efter årsskiftet 2009/2010, dvs vid årsskiftet 2013/2014.
c) För att få företagets maximala vinst sätter vi in \( t_{max} = 4 \, \) i vinstfunktionen:
- \[ V(t) = -3\,t^3 + 27\,t^2 - 72\,t + 60 \]
- \[ V(t_{max}) = V(4) = -3\cdot 4^3 + 27\cdot 4^2 - 72\cdot 4 + 60 = 12 \]
Alltså är företagets maximala vinst \( 12\,000 \) kr som antas vid årsskiftet 2013/2014.
Begreppsförklaringar
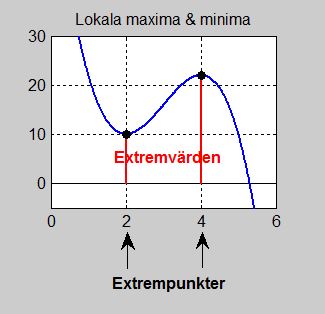 |
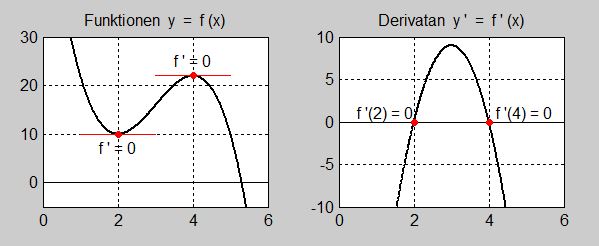
Lokala maxima och minima är punkter (•) som har största resp. minsta \( \, y\)-värden i sin närmaste omgivning.
Med maxima och minima menas i detta kapitel alltid lokala maxima/minima. Ordet lokalt utelämnas ofta. Båda tillsammans heter extrema eller extremvärden. På bilden till vänster har vi två extremvärden: \( \, 10 \, \) och \( \, 22 \, \). De punkter på \( \, x\)-axeln för vilka dessa extremvärden antas heter extrempunkter, på bilden: \( \, 2 \, \) och \( \, 4 \, \). Minimipunktens koordinater är: \( \, (2, 10) \, \). Maximipunktens koordinater är: \( \, (4, 22) \, \).
Med kring \( \, {\color{Red} a} \, \) i Regler om max/min med teckenstudium menas i en tillräckligt liten omgivning av \( \, {\color{Red} a} \, \). Detta betyder i praktiken att man ska undersöka ett ev. teckenbyte i en omgivning som är så nära \( \, a \) som möjligt. Hur stor exakt en tillräckligt liten omgivning av\( \, a \,\) ska vara beror på den aktuella funktionen \( \, f(x)\):s egenskaper. |
OBS! Det finns punkter där derivatan är \( \, 0 \), utan att dessa punkter är extrempunkter. De behandlas i nästa avsnitt.
Copyright © 2011-2016 Taifun Alishenas. All Rights Reserved.