Skillnad mellan versioner av "Potenser"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 9: | Rad 9: | ||
__NOTOC__ <!-- __TOC__ --> | __NOTOC__ <!-- __TOC__ --> | ||
| − | == <b><span style="color:#931136"> | + | == <b><span style="color:#931136">Vad är en potens?</span></b> == |
<div class="exempel"> | <div class="exempel"> | ||
[[Image: Hur raknar du Potenser 20.jpg]] | [[Image: Hur raknar du Potenser 20.jpg]] | ||
| Rad 18: | Rad 18: | ||
<div class="tolv"> <!-- tolv1 --> | <div class="tolv"> <!-- tolv1 --> | ||
| − | + | Felet beror på att man blandar ihop två olika räkneoperationer: multiplikationen med <strong><span style="color:red">upphöjt till</span></strong>. | |
| − | Hjärnan associerar <math> \, 2 \, </math> och <math> \, 3 \, </math> blind till multiplikationstabellen vilket ger <math> \, 6 \, </math>. I själva verket betyder <math> \, 2\,^{\color{Red} 3} \, </math> inte <math> \, 2 \cdot 3 \, </math> utan <math> \, \underbrace{2 \cdot 2 \cdot 2}_{{\color{Red} 3}\;\times} \, </math>. | + | Hjärnan associerar <math> \, 2 \, </math> och <math> \, 3 \, </math> blind till multiplikationstabellen vilket ger <math> \, 6 \, </math>. |
| + | |||
| + | I själva verket betyder <math> \, 2\,^{\color{Red} 3} \, </math> inte <math> \, 2 \cdot 3 \, </math> utan <math> \, \underbrace{2 \cdot 2 \cdot 2}_{{\color{Red} 3}\;\times} \, </math> och är en:. | ||
</div> <!-- tolv1 --> | </div> <!-- tolv1 --> | ||
| − | |||
| − | |||
| − | + | <table> | |
| + | <tr> | ||
| + | <td><div class="border-divblue"><big> | ||
| + | <b>Potens</b> | ||
| − | + | ::<math> 2\,^{\color{Red} 3} \; = \;\; \underbrace{2 \, \cdot \, 2 \, \cdot \, 2}_{{\color{Red} 3}\;\times} </math> | |
| + | <b>Upprepad multiplikation av </b> | ||
| − | + | <b><math>2 \, </math> med sig själv, <math> \, {\color{Red} 3} \, </math> gånger.</b> | |
| + | </big></div> | ||
| + | </td> | ||
| + | <td> [[Image: Potens Bas Exponent_80.jpg]]</td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | + | <div class="tolv"> <!-- tolv2 --> | |
| − | + | <math> \, 2\,^3 \, </math> läses <math> \, {\color{Red} 2} </math> <strong><span style="color:red">upphöjt till</span></strong><math> \, {\color{Red} 3} \, </math> och kallas för <strong><span style="color:red">potens</span></strong>. <math> \, 2\, </math> heter <strong><span style="color:red">basen</span></strong> och <math> \, 3 \, </math> <strong><span style="color:red">exponenten</span></strong>. | |
| + | Exponenten <math> \, {\color{Red} 3} \, </math> är inget tal i vanlig bemärkelse utan endast en information om att <math> \, 2 \, </math> ska multipliceras <math> \, {\color{Red} 3} \, </math> gånger med sig själv (jfr. [[1.2_Räkneordning#Varf.C3.B6r_g.C3.A5r_multiplikation_f.C3.B6re_addition.3F|<strong><span style="color:blue">upprepad addition</span></strong>]]). | ||
| + | </div> <!-- tolv2 --> | ||
| − | |||
| − | |||
| − | :: | + | <div class="exempel"> <!-- exempel1 --> |
| + | == <b><span style="color:#931136">Exempel 1</span></b> == | ||
| + | <big> | ||
| + | Förenkla<span style="color:black">:</span> <math> \qquad \displaystyle{2\,^3 \cdot \; 2\,^5 \over 2\,^4} </math> | ||
| − | |||
| − | + | <strong><span style="color:#931136">Lösning:</span></strong> <math> \qquad \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \over 2 \cdot 2 \cdot 2 \cdot 2} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot \cancel{2 \cdot 2 \cdot 2 \cdot 2} \over \cancel{2 \cdot 2 \cdot 2 \cdot 2}} \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} </math> | |
| − | :::: | + | :::::::::::::::::OBS! Förenkla alltid först, räkna sedan! |
| − | + | Snabbare<span style="color:black">:</span> <math> \qquad\!\! \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, 2\,^{3\,+\,5\,-\,4} \, = \, 2\,^4 \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} </math> | |
| + | </big> | ||
| + | </div> <!-- exempel1 --> | ||
| − | ::::<big><math> a^2 \cdot a^3 \; = \; a^{2+3} = \; a^5</math></big> | + | |
| − | </div> <!-- | + | <div class="tolv"> <!-- tolv2 --> |
| + | För att förstå den snabbare lösningen se [[1.7_Potenser#Potenslagarna|<strong><span style="color:blue">potenslagarna</span></strong>]]. | ||
| + | </div> <!-- tolv2 --> | ||
| + | |||
| + | |||
| + | == <b><span style="color:#931136">Potens med positiva heltalsexponenter</span></b> == | ||
| + | <div class="tolv"> <!-- tolv1 --> | ||
| + | |||
| + | Potensen <math> \, a\,^x \, </math> kan, om exponenten <math> \, {\color{Red} x} \, </math> är ett positivt heltal och basen <math> a\, </math> ett tal <math> \neq 0 </math>, definieras som upprepad multiplikation av <math> \, a \, </math> med sig själv, <math> \, {\color{Red} x} \, </math> gånger: | ||
| + | |||
| + | |||
| + | ::::<big><math> a^{\color{Red} x} = \underbrace{a \cdot a \cdot a \cdot \quad \ \cdots \quad \cdot a}_{{\color{Red} x}\;{\rm gånger}} </math></big> | ||
| + | </div> <!-- tolv1 --> | ||
| + | |||
| + | |||
| + | <div class="exempel"> <!-- exempel2 --> | ||
| + | == <b><span style="color:#931136">Exempel 2</span></b> == | ||
| + | <big> | ||
| + | Förenkla<span style="color:black">:</span> <big><math> \quad\;\; a\,^2 \, \cdot \, a\,^3 </math></big> | ||
| + | |||
| + | |||
| + | <strong><span style="color:#931136">Lösning:</span></strong> | ||
| + | |||
| + | ::::<big><math> a\,^2 \cdot a\,^3 \; = \; \underbrace{a \cdot a}_{2\;\times} \; \cdot \; \underbrace{a \cdot a \cdot a}_{3\;\times} \; = \; \underbrace{a \cdot a \cdot a \cdot a \cdot a}_{{\color{Red} 5}\;\times} \; = \; a\,^{\color{Red} 5}</math></big> | ||
| + | |||
| + | Snabbare: | ||
| + | |||
| + | ::::<big><math> a\,^2 \cdot a\,^3 \; = \; a\,^{2\,+\,3} = \; a\,^{\color{Red} 5} </math></big> | ||
| + | </big> | ||
| + | </div> <!-- exempel2 --> | ||
<div class="tolv"> <!-- tolv2 --> | <div class="tolv"> <!-- tolv2 --> | ||
| − | + | Den snabbare lösningen är ett exempel på den första potenslagen: | |
</div> <!-- tolv2 --> | </div> <!-- tolv2 --> | ||
| Rad 62: | Rad 104: | ||
<div class="tolv"> <!-- tolv3 --> | <div class="tolv"> <!-- tolv3 --> | ||
| − | Följande lagar gäller för potenser där basen <math> a\, </math> är ett tal <math> \neq 0 </math>, exponenterna <math> \, x \, </math> och <math> \, y \, </math> | + | Följande lagar gäller för potenser där basen <math> a\, </math> är ett tal <math> \neq 0 </math>, exponenterna <math> \, x \, </math> och <math> \, y \, </math> godtyckliga tal och <math> m,\,n </math> heltal (<math> n\neq 0 </math>): |
</div> <!-- tolv3 --> | </div> <!-- tolv3 --> | ||
| Rad 88: | Rad 130: | ||
<div class="tolv"> <!-- tolv3a --> | <div class="tolv"> <!-- tolv3a --> | ||
| − | För enkelhets skull definierades potensbegreppet inledningsvis endast för positiva heltalsexponenter <math> \, x \, </math> och <math> \, y </math>. Men potenslagarna gäller även för negativa och rationella exponenter | + | För enkelhets skull definierades potensbegreppet inledningsvis endast för positiva heltalsexponenter <math> \, x \, </math> och <math> \, y </math>. Men potenslagarna gäller även för negativa och [[1.7_Potenser#Potenser_med_rationella_exponenter|<strong><span style="color:blue">rationella exponenter</span></strong>]]. I formuleringen "negativ exponent" antas <math> \, x > 0 </math>. |
</div> <!-- tolv3a --> | </div> <!-- tolv3a --> | ||
| − | == <b><span style="color:#931136">Bevis(idéer) för några potenslagar</span></b> == | + | == <b><span style="color:#931136">Bevis(idéer) och exempel för några potenslagar</span></b> == |
<div class="tolv"> <!-- tolv4 --> | <div class="tolv"> <!-- tolv4 --> | ||
'''Påstående (Första potenslagen)''': | '''Påstående (Första potenslagen)''': | ||
| − | ::::<big><math> a^x \cdot a^y \; = \; a\,^{x \, + \, y} </math></big> | + | ::::<big><math> a\,^x \cdot a\,^y \; = \; a\,^{x \, + \, y} </math></big> |
'''Bevisidé''': | '''Bevisidé''': | ||
| Rad 103: | Rad 145: | ||
Påståendet kan bevisas genom att använda potensens definition: | Påståendet kan bevisas genom att använda potensens definition: | ||
| − | ::::<big><math> a^{\color{Red} x} \cdot a^{\color{Red} y} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} x}\;\times} \; \cdot \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} y}\;\times} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} {x+y}}\;\times} \; = \; a^{{\color{Red} {x+y}}} </math></big> | + | ::::<big><math> a\,^{\color{Red} x} \cdot a\,^{\color{Red} y} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} x}\;\times} \; \cdot \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} y}\;\times} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} {x\,+\,y}}\;\times} \; = \; a\,^{{\color{Red} {x\,+\,y}}} </math></big> |
---- | ---- | ||
| Rad 110: | Rad 152: | ||
'''Påstående (Andra potenslagen)''': | '''Påstående (Andra potenslagen)''': | ||
| − | ::::<big><math> \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} </math></big> | + | ::::<big><math> \displaystyle {a\,^x \over a\,^y} \; = \; a\,^{x \, - \, y} </math></big> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</div> <!-- tolv1 --> | </div> <!-- tolv1 --> | ||
| − | <div class=" | + | <div class="exempel"> <!-- exempel3 --> |
| − | + | == <b><span style="color:#931136">Exempel 3</span></b> == | |
| + | <big> | ||
| + | ::::<big><math> \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; {a \cdot a \cdot a \cdot a \cdot a \; \over \; a \cdot a \cdot a} \; = \; {a \cdot a \cdot \cancel{a \cdot a \cdot a} \; \over \; \cancel{a \cdot a \cdot a}} \; = \; a \cdot a \; = \; a\,^2 </math></big> | ||
| − | : | + | Snabbare med andra potenslagen: |
| − | + | ::::<big><math> \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; a\,^{{\color{Red} {5\,-\,3}}} \; = \; a\,^2 </math></big> | |
| − | + | </big> | |
| − | ::::<big><math> \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; a\,^{{\color{Red} {5-3}}} \; = \; a\,^2 </math></big> | + | </div> <!-- exempel3 --> |
| − | </div> <!-- | + | |
| Rad 172: | Rad 207: | ||
| − | <div class=" | + | <div class="exempel"> <!-- exempel4 --> |
| − | == | + | == <b><span style="color:#931136">Exempel på potenser med negativa exponenter</span></b> == |
| + | <big> | ||
| − | ::::<math> \ | + | ::::<big><math> \displaystyle{a^{-1} \, = \, {1 \over a^1} \, = \, {1 \over a}} </math></big> |
| − | |||
| − | ::::<math> \ | + | ::::<big><math> \displaystyle{a^{-2} \, = \, {1 \over a^2} \, = \, {1 \over a \cdot a}} </math></big> |
| − | </div> <!-- | + | |
| + | |||
| + | ::::<big><math> \displaystyle{a^{-3} \, = \, {1 \over a^3} \, = \, {1 \over a \cdot a \cdot a}} </math></big> | ||
| + | </big> | ||
| + | </div> <!-- exempel4 --> | ||
| Rad 188: | Rad 227: | ||
| − | <div class=" | + | <div class="exempel"> <!-- exempel4 --> |
| − | == | + | == <b><span style="color:#931136">Varför är <math> \; 5\,^0 \, = \, 1 \; </math>?</span></b> == |
| + | <big> | ||
::::<math> \;\; 5^4 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \cdot 5 </math> | ::::<math> \;\; 5^4 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \cdot 5 </math> | ||
| Rad 210: | Rad 250: | ||
Att <math> \; {\color{Red} 1} </math>-orna följer med hela tiden beror på att multiplikationens ''enhet'' är <math> \, {\color{Red} 1} </math>, dvs <math> \, a \cdot {\color{Red} 1} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 1} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5^0}} \, </math> då alla <math> \, 5</math>-or har försvunnit. | Att <math> \; {\color{Red} 1} </math>-orna följer med hela tiden beror på att multiplikationens ''enhet'' är <math> \, {\color{Red} 1} </math>, dvs <math> \, a \cdot {\color{Red} 1} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 1} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5^0}} \, </math> då alla <math> \, 5</math>-or har försvunnit. | ||
| − | </div> <!-- | + | </big> |
| + | </div> <!-- exempel4 --> | ||
| Rad 218: | Rad 259: | ||
| − | <div class=" | + | <div class="exempel"> <!-- exempel5 --> |
| − | == | + | == <b><span style="color:#931136">Varför är <math> \; 5 \cdot 0 \, = \, 0 \; </math>?</span></b> == |
| + | <big> | ||
::::<math> \;\; 5 \cdot 4 \; = \; {\color{Red} 0} + 5 + 5 + 5 + 5 </math> | ::::<math> \;\; 5 \cdot 4 \; = \; {\color{Red} 0} + 5 + 5 + 5 + 5 </math> | ||
| Rad 240: | Rad 282: | ||
Att <math> \; {\color{Red} 0} </math>-orna följer med hela tiden beror på att additionens ''enhet'' är <math> \, {\color{Red} 0} </math>, dvs <math> \, a + {\color{Red} 0} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 0} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5 \cdot 0}} \, </math> då alla <math> \, 5</math>-or har försvunnit. | Att <math> \; {\color{Red} 0} </math>-orna följer med hela tiden beror på att additionens ''enhet'' är <math> \, {\color{Red} 0} </math>, dvs <math> \, a + {\color{Red} 0} \, = \, a </math>. Därför blir endast <math> \, {\color{Red} 0} \, </math> kvar, när vi kommer till <math> \, {\color{Red} {5 \cdot 0}} \, </math> då alla <math> \, 5</math>-or har försvunnit. | ||
| − | </div> <!-- | + | </big> |
| + | </div> <!-- exempel5 --> | ||
== <b><span style="color:#931136">Potenser med rationella exponenter</span></b> == | == <b><span style="color:#931136">Potenser med rationella exponenter</span></b> == | ||
<div class="tolv"> <!-- tolv6 --> | <div class="tolv"> <!-- tolv6 --> | ||
| − | Potenser med | + | Potenser med exponenter som är [[1.1_Om_tal#Olika_typer_av_tal|rationella tal]] (bråktal) kan användas för att beräkna (högre) rötter. |
| − | '''Påstående ( | + | '''Påstående (högre rötter)''': |
:::<big><math> a^{1 \over n} \; = \; \sqrt[n]{a} \; </math></big> <math> , \qquad n\neq 0 </math> | :::<big><math> a^{1 \over n} \; = \; \sqrt[n]{a} \; </math></big> <math> , \qquad n\neq 0 </math> | ||
| Rad 266: | Rad 309: | ||
:::<big><math> \displaystyle a^{1 \over 3} \; = \; \sqrt[3]{a} </math></big> | :::<big><math> \displaystyle a^{1 \over 3} \; = \; \sqrt[3]{a} </math></big> | ||
| − | Denna bevisidé kan vidareutvecklas till det allmänna fallet för alla heltal <math> m\, </math> och <math> n\neq 0 </math> | + | Denna bevisidé kan vidareutvecklas till det allmänna fallet för alla heltal <math> m\, </math> och <math> n\neq 0 \, </math> '''(Lagen om rationell exponent)''': |
| − | + | ||
| − | ''' | + | |
:::<big><math> a^{m \over n} \; = \; \sqrt[n]{a^m} </math></big> | :::<big><math> a^{m \over n} \; = \; \sqrt[n]{a^m} </math></big> | ||
Versionen från 23 juni 2015 kl. 10.06
| <-- Till Polynom | Genomgång | Övningar |
Vad är en potens?
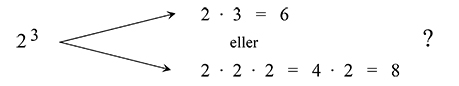 \[ {\rm {\color{Red} {OBS!\quad Vanligt\,fel:}}} \quad\; 2\,^3 \; = \; 6 \]
\[ {\rm {\color{Red} {OBS!\quad Vanligt\,fel:}}} \quad\; 2\,^3 \; = \; 6 \]
\[ \qquad\quad\;\, {\rm Rätt:} \qquad\qquad\! 2\,^3 \; = \; 2 \cdot 2 \cdot 2 \; = \; 4 \cdot 2 \; = \; 8 \]
Felet beror på att man blandar ihop två olika räkneoperationer: multiplikationen med upphöjt till.
Hjärnan associerar \( \, 2 \, \) och \( \, 3 \, \) blind till multiplikationstabellen vilket ger \( \, 6 \, \).
I själva verket betyder \( \, 2\,^{\color{Red} 3} \, \) inte \( \, 2 \cdot 3 \, \) utan \( \, \underbrace{2 \cdot 2 \cdot 2}_{{\color{Red} 3}\;\times} \, \) och är en:.
Potens
Upprepad multiplikation av \(2 \, \) med sig själv, \( \, {\color{Red} 3} \, \) gånger. |
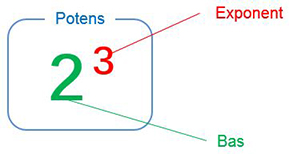 |
\( \, 2\,^3 \, \) läses \( \, {\color{Red} 2} \) upphöjt till\( \, {\color{Red} 3} \, \) och kallas för potens. \( \, 2\, \) heter basen och \( \, 3 \, \) exponenten.
Exponenten \( \, {\color{Red} 3} \, \) är inget tal i vanlig bemärkelse utan endast en information om att \( \, 2 \, \) ska multipliceras \( \, {\color{Red} 3} \, \) gånger med sig själv (jfr. upprepad addition).
Exempel 1
Förenkla: \( \qquad \displaystyle{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \)
Lösning: \( \qquad \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \over 2 \cdot 2 \cdot 2 \cdot 2} \, = \, {2 \cdot 2 \cdot 2 \quad \cdot \quad 2 \cdot \cancel{2 \cdot 2 \cdot 2 \cdot 2} \over \cancel{2 \cdot 2 \cdot 2 \cdot 2}} \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} \)
- OBS! Förenkla alltid först, räkna sedan!
Snabbare: \( \qquad\!\! \displaystyle{{2\,^3 \cdot \; 2\,^5 \over 2\,^4} \, = \, 2\,^{3\,+\,5\,-\,4} \, = \, 2\,^4 \, = \, 2 \cdot 2 \cdot 2 \cdot 2 \, = \, 4 \cdot 4 \, = \, 16} \)
För att förstå den snabbare lösningen se potenslagarna.
Potens med positiva heltalsexponenter
Potensen \( \, a\,^x \, \) kan, om exponenten \( \, {\color{Red} x} \, \) är ett positivt heltal och basen \( a\, \) ett tal \( \neq 0 \), definieras som upprepad multiplikation av \( \, a \, \) med sig själv, \( \, {\color{Red} x} \, \) gånger:
- \( a^{\color{Red} x} = \underbrace{a \cdot a \cdot a \cdot \quad \ \cdots \quad \cdot a}_{{\color{Red} x}\;{\rm gånger}} \)
Exempel 2
Förenkla: \( \quad\;\; a\,^2 \, \cdot \, a\,^3 \)
Lösning:
- \( a\,^2 \cdot a\,^3 \; = \; \underbrace{a \cdot a}_{2\;\times} \; \cdot \; \underbrace{a \cdot a \cdot a}_{3\;\times} \; = \; \underbrace{a \cdot a \cdot a \cdot a \cdot a}_{{\color{Red} 5}\;\times} \; = \; a\,^{\color{Red} 5}\)
Snabbare:
- \( a\,^2 \cdot a\,^3 \; = \; a\,^{2\,+\,3} = \; a\,^{\color{Red} 5} \)
Den snabbare lösningen är ett exempel på den första potenslagen:
Potenslagarna
Följande lagar gäller för potenser där basen \( a\, \) är ett tal \( \neq 0 \), exponenterna \( \, x \, \) och \( \, y \, \) godtyckliga tal och \( m,\,n \) heltal (\( n\neq 0 \)):
Första potenslagen: \( \qquad\qquad\quad\;\, a^x \cdot a^y \; = \; a\,^{x \, + \, y} \qquad\qquad \)
Andra potenslagen: \( \qquad\qquad\qquad\quad \displaystyle {a^x \over a^y} \; = \; a\,^{x \, - \, y} \qquad\qquad \)
Tredje potenslagen: \( \qquad\qquad\qquad \displaystyle {(a^x)^y} \; = \; a\,^{x \, \cdot \, y} \qquad\qquad \)
Lagen om nollte potens: \( \qquad\qquad\qquad\! a\,^0 \; = \; 1 \qquad\qquad \)
Lagen om negativ exponent: \( \qquad\qquad a\,^{-x} \; = \; \displaystyle {1 \over a\,^x} \qquad\qquad \)
Lagen om rationell exponent: \( \qquad\qquad a^{m \over n} \; = \; \sqrt[n]{a^m} \qquad\qquad \)
Specialfall \(m=1\) (högre rötter): \( \qquad\quad\;\, a^{1 \over n} \; = \; \sqrt[n]{a} \qquad\qquad \)
Potens av en produkt: \( \qquad\qquad\;\;\, (a \cdot b)\,^x \; = \; a\,^x \cdot b\,^x \qquad\qquad \)
Potens av en kvot: \( \qquad\qquad\qquad \left(\displaystyle {a \over b}\right)^x \; = \; \displaystyle {a\,^x \over b\,^x} \qquad\qquad \)
För enkelhets skull definierades potensbegreppet inledningsvis endast för positiva heltalsexponenter \( \, x \, \) och \( \, y \). Men potenslagarna gäller även för negativa och rationella exponenter. I formuleringen "negativ exponent" antas \( \, x > 0 \).
Bevis(idéer) och exempel för några potenslagar
Påstående (Första potenslagen):
- \( a\,^x \cdot a\,^y \; = \; a\,^{x \, + \, y} \)
Bevisidé:
Påståendet kan bevisas genom att använda potensens definition:
- \( a\,^{\color{Red} x} \cdot a\,^{\color{Red} y} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} x}\;\times} \; \cdot \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} y}\;\times} \; = \; \underbrace{a \cdot a \cdot \; \ \cdots \; \cdot a}_{{\color{Red} {x\,+\,y}}\;\times} \; = \; a\,^{{\color{Red} {x\,+\,y}}} \)
Påstående (Andra potenslagen):
- \( \displaystyle {a\,^x \over a\,^y} \; = \; a\,^{x \, - \, y} \)
Exempel 3
- \( \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; {a \cdot a \cdot a \cdot a \cdot a \; \over \; a \cdot a \cdot a} \; = \; {a \cdot a \cdot \cancel{a \cdot a \cdot a} \; \over \; \cancel{a \cdot a \cdot a}} \; = \; a \cdot a \; = \; a\,^2 \)
Snabbare med andra potenslagen:
- \( \displaystyle {a\,^{\color{Red} 5} \over a\,^{\color{Red} 3}} \; = \; a\,^{{\color{Red} {5\,-\,3}}} \; = \; a\,^2 \)
Påstående (Lagen om nollte potens):
- \( a^0 \; = \; 1 \)
Bevis:
Påståendet kan bevisas genom att använda andra potenslagen:
- \( \displaystyle{a^x \over a^x} \; = \; a^{x-x} \; = \; a^0 \)
Å andra sidan vet vi att ett bråk med samma täljare som nämnare har värdet \( \, 1 \):
- \( \displaystyle{a^x \over a^x} \; = \; 1 \)
Av raderna ovan följer påståendet:
- \( a^0 \; = \; 1 \)
Potenser med negativa exponenter
Påstående (Lagen om negativ exponent, \( \, x > 0 \)):
- \( a^{-x} = \displaystyle{1 \over a^x} \)
Bevis:
Påståendet kan bevisas genom att använda den ovan bevisade lagen om nollte potensen (baklänges) samt andra potenslagen:
- \( \displaystyle{1 \over a^x} \; = \; \displaystyle{a^0 \over a^x} \; = \; a^{0-x} \; = \; a^{-x} \)
Vi får påståendet, fast baklänges.
Exempel på potenser med negativa exponenter
- \( \displaystyle{a^{-1} \, = \, {1 \over a^1} \, = \, {1 \over a}} \)
- \( \displaystyle{a^{-2} \, = \, {1 \over a^2} \, = \, {1 \over a \cdot a}} \)
- \( \displaystyle{a^{-3} \, = \, {1 \over a^3} \, = \, {1 \over a \cdot a \cdot a}} \)
Att potenser med negativa exponenter är en naturlig fortsättning på potenser med positiva exponenter med nollte potensen däremellan illustrerar följande exempel:
Varför är \( \; 5\,^0 \, = \, 1 \; \)?
- \[ \;\; 5^4 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \cdot 5 \]
- \[ \;\; 5^3 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \cdot 5 \]
- \[ \;\; 5^2 \; = \; {\color{Red} 1} \cdot 5 \cdot 5 \]
- \[ \;\; 5^1 \; = \; {\color{Red} 1} \cdot 5 \]
- \[ \;\; {\color{Red} {5^0 \; = \; 1}} \]
- \[ \;\; 5^{-1} \; = \; \displaystyle{{\color{Red} 1} \over 5} \]
- \[ \;\; 5^{-2} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5} \]
- \[ \;\; 5^{-3} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5} \]
- \[ \;\; 5^{-4} \; = \; \displaystyle{{\color{Red} 1} \over 5 \cdot 5 \cdot 5 \cdot 5 } \]
Att \( \; {\color{Red} 1} \)-orna följer med hela tiden beror på att multiplikationens enhet är \( \, {\color{Red} 1} \), dvs \( \, a \cdot {\color{Red} 1} \, = \, a \). Därför blir endast \( \, {\color{Red} 1} \, \) kvar, när vi kommer till \( \, {\color{Red} {5^0}} \, \) då alla \( \, 5\)-or har försvunnit.
Jämför med:
Varför är \( \; 5 \cdot 0 \, = \, 0 \; \)?
- \[ \;\; 5 \cdot 4 \; = \; {\color{Red} 0} + 5 + 5 + 5 + 5 \]
- \[ \;\; 5 \cdot 3 \; = \; {\color{Red} 0} + 5 + 5 + 5 \]
- \[ \;\; 5 \cdot 2 \; = \; {\color{Red} 0} + 5 + 5 \]
- \[ \;\; 5 \cdot 1 \; = \; {\color{Red} 0} + 5 \]
- \[ \;\; {\color{Red} {5 \cdot 0 \; = \; 0}} \]
- \[ \;\; 5 \cdot (-1) \; = \; {\color{Red} 0} - 5 \]
- \[ \;\; 5 \cdot (-2) \; = \; {\color{Red} 0} - 5 - 5 \]
- \[ \;\; 5 \cdot (-3) \; = \; {\color{Red} 0} - 5 - 5 - 5 \]
- \[ \;\; 5 \cdot (-4) \; = \; {\color{Red} 0} - 5 - 5 - 5 - 5 \]
Att \( \; {\color{Red} 0} \)-orna följer med hela tiden beror på att additionens enhet är \( \, {\color{Red} 0} \), dvs \( \, a + {\color{Red} 0} \, = \, a \). Därför blir endast \( \, {\color{Red} 0} \, \) kvar, när vi kommer till \( \, {\color{Red} {5 \cdot 0}} \, \) då alla \( \, 5\)-or har försvunnit.
Potenser med rationella exponenter
Potenser med exponenter som är rationella tal (bråktal) kan användas för att beräkna (högre) rötter.
Påstående (högre rötter):
- \( a^{1 \over n} \; = \; \sqrt[n]{a} \; \) \( , \qquad n\neq 0 \)
Bevisidé:
Vi tar specialfallet \( n=3 \), multiplicerar \( a \)\(^{1 \over 3} \) tre gånger med sig själv och använder potenslagen om produkt av potenser med samma bas:
- \( \displaystyle a^{1 \over 3} \cdot a^{1 \over 3} \cdot a^{1 \over 3} \; = \; a^{{1 \over 3} + {1 \over 3} + {1 \over 3}} \; = \; a^{3 \over 3} \; = \; a^1 \; = \; a \)
Definitionen för 3:e roten ur \( a \) är:
\( \qquad\quad \displaystyle \sqrt[3]{a} \; = \; \) Tal som 3 gånger multiplicerat med sig själv ger \( a \).
Men enligt ovan är det tal som 3 gånger med sig själv ger \( a \), just \( a \) \(^{1 \over 3} \). Alltså måste detta tal vara lika med 3:e roten ur \( a \):
- \( \displaystyle a^{1 \over 3} \; = \; \sqrt[3]{a} \)
Denna bevisidé kan vidareutvecklas till det allmänna fallet för alla heltal \( m\, \) och \( n\neq 0 \, \) (Lagen om rationell exponent):
- \( a^{m \over n} \; = \; \sqrt[n]{a^m} \)
Potensekvationer
Anta i fortsättningen att \( \, x \, \) är en okänd variabel och \( b\, \) och \( c\, \) givna konstanter \( \neq 0 \) .
- Funktioner av typ \( y = x^3\, \) kallas potensfunktioner, generellt \( \; y = c \cdot x^b\, \).
- Ekvationer av typ \( x^3\, = 8 \) kallas potensekvationer, generellt \( \; x^b\, = c \).
I potensfunktioner och -ekvationer förekommer \( \, x \, \) i basen. Potensekvationer löses genom rotdragning. För t.ex. potensekvationen \( x^3\, = 8 \) finns det två olika sätt att beskriva lösningen via rotdragning:
- \[\begin{align} x^3 & = 8 \qquad & | \; \sqrt[3]{\;\;} \\ \sqrt[3]{x^3} & = \sqrt[3]{8} \\ x & = 2 \\ \end{align}\]
Alternativt (med rationell exponent):
- \[\begin{align} x^3 & = 8 \qquad & | \; (\;\;\;)^{1 \over 3} \; \text{samma som} \; \sqrt[3]{\;\;} \\ (x^3)^{1 \over 3} & = 8^{1 \over 3} \\ x^{3\cdot{1 \over 3}} & = 8^{1 \over 3} \\ x & = 2 \\ \end{align}\]
Det alternativa sättet att lösa ekvationen ovan visar att rötter även kan uppfattas och skrivas som potenser med rationella exponenter.
Internetlänkar
http://www.youtube.com/watch?v=iYgG4LUqXks
http://www.webbmatte.se/gym/arabiska/2/2_8_4sv.html
http://www.webbmatte.se/gym/arabiska/2/2_8_3sv.html
http://wiki.math.se/wikis/forberedandematte1/index.php/1.3_%C3%96vningar
Copyright © 2010-2015 Math Online Sweden AB. All Rights Reserved.