Skillnad mellan versioner av "3.5 Extremvärdesproblem"

Versionen från 9 juni 2015 kl. 00.23

Genomgång

Övningar

Diagnosprov kap 3 Anv. av deriv.

Lösningar till diagnosprov kap 3

Lektion 33 Extremvärdesproblem I

Lektion 34 Extremvärdesproblem II

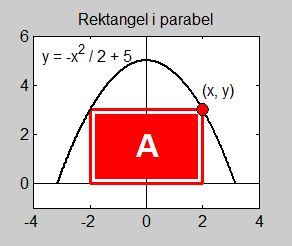
Exempel 1 Rektangel i parabel

En rektangel är inbunden i en parabel vars ekvation är given:

\[ y \, = \, -\,{\, x^2 \over 2} \, + \, 5 \qquad {\rm med} \qquad y \, \geq \, 0 \]

Punkten \( \, (x,\,y) \, \) rör sig på parabeln, se figuren. Placera den så

att rektangelns area \( \, A \, \) blir så stor som möjligt.

a) Ställ upp rektangelns area som en funktion av \( \, x \, \) dvs \( \, A(x) \, \).

b) Bestäm \( \, x \, \) så att \( \, A(x) \, \) antar ett maximum.

c) Beräkna rektangelns maximala area.

Lösning:

a) Rektangelns area kan skrivas som \( \quad A\,(x, \, {\color{Red} y}) \; = \; 2 \, \cdot x \, \cdot \, {\color{Red} y} \)

Men \( \, A\,(x, \, {\color{Red} y}) \, \) är en funktion av två variabler som vi inte kan hantera. För att skriva om den till en funktion \( \, A\,(x) \, \) av endast en variabel, nämligen \( \, x \, \), måste \( \, {\color{Red} y} \, \) elimineras.

Det gör vi genom att utnyttja sambandet mellan \( \, x \, \) och \( \, {\color{Red} y} \, \) som är givet av parabelns ekvation. Rektangelns "rörliga" hörn måste alltid ligga på parabeln. Därför måste dess koordinater \( \, (x,\,{\color{Red} y}) \, \) uppfylla parabelns ekvation som kallas för problemets bivillkor:

\( \displaystyle {\color{Red} y} \, = \, -\,{\, x^2 \over 2} \, + \, 5 \)

Bivillkor för ett extremvärdesproblem:

Ett extremvärdesproblems bivillkor är ett samband mellan problemets variabler och bestäms av problemets givna

geometriska eller andra egenskaper. Ibland kallas det även för tvångsvillkor (eng. constraint).

Tvångsvillkor, därför att man är tvungen att uppfylla bivillkoret.

I vårt exempel är bivillkoret parabelns ovan angivna ekvation, för punkten \( \, (x,\,y) \, \) måste följa parabeln.

Vi använder detta bivillkor för att skriva om rektangelns area från en funktion av två variabler till en funktion av endast en variabel.

Därför sätter vi in bivillkoret i \( \; A\,(x, \, {\color{Red} y}) \, = \, 2\cdot x \cdot {\color{Red} y} \; \) för att eliminera \( \, {\color{Red} y} \,\). På så sätt får vi ett uttryck för rektangelns area som endast beror av \( \, x \):

\[ A\,(x, \, {\color{Red} y}) \, = \, 2 \cdot x \cdot {\color{Red} y} \, = \, 2 \cdot x \cdot \left({\color{Red} {-\,{\, x^2 \over 2} \, + \, 5}}\right) \, = \, -\,x^3 \, + \, 10\,x \]

Den erhållna funktionen av en variabel kallas för problemets målfunktion:

\( A\,(x) \, = \, \displaystyle -\,x^3 \, + \, 10\,x \)

med definitionsmängden: \( \quad 0 \, \leq \, x \, \leq \, \sqrt{10} \)

Det är denna målfunktion som ska maximeras. Definitionsintervallets vänstra ända \( \, 0 \, \) är motiverad av att arean och därmed \( \, x \, \) inte kan bli negativ.

Definitionsintervallets högra ända \( \, \sqrt{10} \, \) ges av parabelns positiva nollställe (se figuren ovan), dvs av lösningen till ekvationen \( \, \displaystyle -{x^2 \over 2} + 5 = 0 \, \).

Målfunktion för ett extremvärdesproblem:

Ett extremvärdesproblems målfunktion är alltid den funktion som ska maximeras eller minimeras (eng. objective function).

Extremvärdesproblem består i regel av ett bivillkor och en målfunktion, där bivillkoret används för att reducera målfunktionen

till en funktion av endast en variabel.

I vårt exempel gäller det att maximera målfunktionen \( \, A\,(x) \, = \, \displaystyle -\,x^3 \, + \, 10\,x \, \) som med hjälp av bivillkoret redan är reducerad till en funktion av endast \( \, x \).

b) Resten av uppgiften \(-\) att maximera \( \, A(x)\) och bestämma rektangelns maximala area \(-\) kan lösas med de metoder vi lärt oss i de förra avsnitten.

För att lösa den första uppgiften börjar vi med att derivera \( \, A(x) \):

\[ A(x) \, = \, -\,x^3 \, + \, 10\,x \]

\[ A'(x) \, = \, -\,3\,x^2 \, + \, 10 \]

\[ A''(x) \, = \, -\,6\,x \]

Derivatans nollställe:

\[\begin{array}{rcrcl} A'(x) & = & -3\,x^2 \, + \, 10 & = & 0 \\ & & 10 & = & 3\,x^2 \\ & & {10 \over 3} & = & x^2 \\ & & x_{1, 2} & = & \sqrt{10 \over 3} \\ & & x_1 & = & 1,83 \\ & & x_2 & = & -1,83 \end{array}\]

Pga målfunktionens definitionsmängd (\( 0 \leq x \leq \sqrt{10} \), se b)) förkastas \( \, x_2 = -1,83 \, \) medan \( \, x_1 = 1,83 \, \) ligger inom definitionsmängden.

Andraderivatans tecken för \( \, x = 1,83 \, \):

\( A''(1,83) = -6 \cdot 1,83 \, < \, 0 \quad \Longrightarrow \quad A(x) \, \) har ett lokalt maximum i \( \, x = 1,83 \, \).

För \( \, x = 1,83 \, {\rm cm} \, \) antar målfunktionen (rektangelns area) sitt maximum.

c) För att bestämma rektangelns maximala area behöver vi bara sätta in \( \, x = 1,83 \, \) i målfunktionen \( \, A(x) \, \) därför att den antar sitt maximum där:

\[ A\,(x) \, = \, \displaystyle -\,x^3 \, + \, 10\,x \]

\[ A(1,83) = -\,1,83^3 \, + \, 10 \cdot 1,83 \, = \, 12,17 \]

Rektangelns maximala area är \( \, 12,17 \, \).

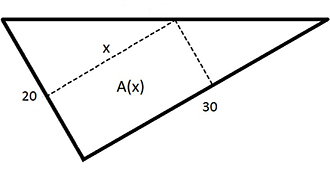
Exempel 2 Glasskiva (rektangel i triangel)

En glasskiva har formen av en rätvinklig triangel med följande mått i cm:

Ur skivan ska en rektangulär glasplatta med maximal area skäras ut.

a) Formulera problemets bivillkor.

b) Ställ upp problemets målfunktion. Ange dess definitionsmängd.

c) Bestäm \( \, x \, \) så att glasplattans area \( \, A(x) \, \) maximeras.

d) Beräkna glasplattans maximala area.

Lösning:

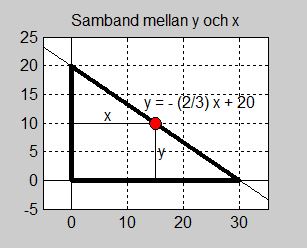
a) Vi inför beteckningen \( \; {\color{Red} y} \; \) för glasplattans andra sida, så att rektangelns area kan skrivas som \( \quad A\,(x, {\color{Red} y}) \; = \; x \; \cdot \; {\color{Red} y} \)

För att skriva om funktionen ovan till en funktion \( \, A\,(x) \, \) av endast en variabel, nämligen \( \, x \, \), måste \( \, {\color{Red} y} \, \) uttryckas med \( \, x \, \), så att \( \, {\color{Red} y} \, \) kan elimineras. Sambandet mellan \( \, x \, \) och \( \, {\color{Red} y} \, \) bestäms av rektangelns "rörliga" hörn som är bundet till triangelns hypotenusa och måste alltid ligga på den.

Vi inför ett koordinatsystem och sätter glasskivan i det, så här:

Triangelns hypotenusa blir då en del av en rät linje.

Punkten \( \, (x, y) \, \) rör sig på denna räta linje vars ekvation är:

\[ {\color{Red} y} \, = \, k\,x \, + \, m \]

Lutningen \( \, k \, = \, \displaystyle {\Delta y \over \Delta x} \, = \, - \, {20 \over 30} \, = \, - \, {2 \over 3} \)

Skärningspunkten med \(\,y\)-axeln: \( \quad m \, = \, 20 \)

Den räta linjens ekvation blir då:

\( \displaystyle {\color{Red} y} \, = \, - \, {2 \over 3}\,x \, + \, 20 \)

Detta samband mellan \( \, x \, \) och \( \, {\color{Red} y} \,\) är problemets bivillkor.

b) Det ovan formulerade bivillkoret för glasskivan sätts in i \( \; A\,(x, {\color{Red} y}) = x \cdot {\color{Red} y} \; \) för att eliminera \( \, {\color{Red} y} \,\) och ställa upp ett uttryck för arean som endast beror av \( \, x \):

\[ A\,(x, \, {\color{Red} y}) \, = \, x \cdot {\color{Red} y} \, = \, x \cdot \left(-\,{2 \over 3}\,x \, + \, 20\right) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x \]

Målfunktionen är:

\( A\,(x) \, = \, \displaystyle -\,{2 \over 3}\,x^2 \, + \, 20\,x \)

med definitionsmängden: \( \quad 0 \, \leq \, x \, \leq \, 30 \,\).

c) För att maximera målfunktionen börjar vi med att derivera den:

\[ A(x) \, = \, -\,{2 \over 3}\,x^2 \, + \, 20\,x \]

\[ A'(x) \, = \, -\,{4 \over 3}\,x \, + \, 20 \]

\[ A''(x) \, = \, -\,{4 \over 3} \]

Derivatans nollställe:

\[\begin{array}{rcrcl} A'(x) & = & -{4 \over 3}\,x + 20 & = & 0 \\ & & 20 & = & {4 \over 3}\,x \\ & & {20 \cdot 3 \over 4} & = & x \\ & & x & = & 15 \end{array}\]

\( \, x = 15 \, \) ligger inom målfunktionens definitionsmängd.

Andraderivatans tecken för \( \, x = 15 \, \):

\( A''(15) = \displaystyle -\,{4 \over 3} \,<\, 0 \quad \Longrightarrow \quad A(x) \, \) har ett lokalt maximum i \( \, x = 15 \, \).

För \( \, x = 15 \, {\rm cm} \, \) antar målfunktionen ett maximum, dvs rektangelns area blir maximal.

d) Eftersom rektangeln får sin största area för \( \, x = 15 \, \) sätter vi in \( \, x = 15 \, \) i målfunktionen för att få största arean:

\[ A\,(x) \, = \, \displaystyle -\,{2 \over 3}\,x^2 \, + \, 20\,x \]

\[ A(15) = -\,{2 \over 3} \cdot 15^2 + 20 \cdot 15 = 150 \]

Glasplattans största area blir \( \, 150 \, {\rm cm}^2 \, \).

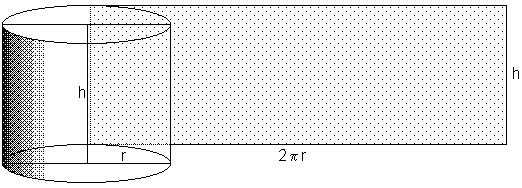
Exempel 3 Konservburk

För att producera en cylinderformad konservburk har man \( \, 500 \, {\rm cm}^2 \, \) plåt

till förfogande (efter spill). Dvs cylinderns begränsningsarea \( \, = \, 500 \, {\rm cm}^2 \, \).

Maximera konservburkens volym.

a) Formulera problemets bivillkor.

b) Ställ upp problemets målfunktion.

c) Bestäm cylinderns radie och höjd så att burkens volym blir maximal.

d) Ange målfunktionens definitionsmängd.

Rita graferna till bivillkoret och målfunktionen.

e) Beräkna konservburkens maximala volym.

f) Vilket samband råder mellan cylinderns radie \( \, r \, \) och dess höjd \( \, h \, \)

när volymen maximeras?

Lösning:

a) Begränsningsarean \( \, A \, = \, 2\,\pi\,r\,h \, + 2\,\pi\,r^2 \, = \, 500 \)

\[\begin{array}{rcl} 2\,\pi\,r\,h \, + 2\,\pi\,r^2 & = & 500 \\ 2\,\pi\,r\,h & = & 500 \, - 2\,\pi\,r^2 \\ h & = & {500 - 2\,\pi\,r^2 \over 2\,\pi\,r} \\ h & = & {500 \over 2\,\pi\,r} \, - \, r \, = \, {250 \over \pi\,r} \, - \, r \end{array}\]

Därmed är bivillkoret:

\( h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \)

b) Cylinderns volym \( \, V \, \) är basytan \( \times \) höjden dvs: \( \qquad\qquad\quad V\,(r, \, {\color{Red} h}) \; = \; \pi \, r^2 \; \cdot \; {\color{Red} h} \, \)

För att skriva om denna funktion av två variabler till en funktion av endast en variabel, sätter vi in bivillkoret från a) i \( \, V\,(r, \, {\color{Red} h}) \, \) och eliminerar \( \, {\color{Red} h} \, \):

\[ V\,(r, \, {\color{Red} h}) \, = \, \pi \, r^2 \; \cdot \; {\color{Red} h} \, = \, \pi\,r^2\cdot \left( {\color{Red} {{250 \over \pi\,r}\,-\, r}} \right) \, = \, {250 \cdot \pi\,r^2 \over \pi\,r} \, - \, \pi\,r^3 \, = \, 250 \cdot r \, - \, \pi\,r^3 \]

Därmed är målfunktionen:

\( V(r) \, = \, 250 \, r \, - \, \pi\,r^3 \)

c) Målfunktionen maximeras:

\[ V(r) \, = \, 250 \, r \, - \, \pi\,r^3 \]

\[ V'(r) \, = \, 250 \, - \, 3\,\pi\,r^2 \]

\[ V''(r) \, = \, -\,6\,\pi\,r \]

Derivatans nollställe:

\[\begin{array}{rcrcl} V'(r) & = & 250 \, - \, 3\,\pi\,r^2 & = & 0 \\ & & 250 & = & 3\,\pi\,r^2 \\ & & {250 \over 3\,\pi} & = & r^2 \\ & & r_{1, 2} & = & \pm\,\sqrt{250 \over 3\,\pi} \\ & & r & = & 5,15 \end{array}\]

\( \, r_2 = -5,15 \, \) förkastas, för radien kan inte bli negativ: \( \, r \, > \, 0 \, \) .

Andraderivatans tecken för \( \, r = 5,15 \, \):

\( V''(5,15) = -6 \,\pi\cdot 5,15 \, < \, 0 \quad \Longrightarrow \quad V(r) \, \) har ett lokalt maximum för \( \, r = 5,15 \, \).

För att få cylinderns höjd när volymen maximeras sätter vi in \( \, r = 5,15 \, \) i bivillkoret från a):

\( h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \, = \, {250 \over \pi\cdot 5,15} \, - \, 5,15 \, = \, 10,30 \)

Cylinderns volym blir maximal för radien \( \; r = 5,15 \, {\rm cm} \; \) och höjden \( \; h = 10,30 \, {\rm cm} \; \).

d) För att bestämma målfunktionens definitionsmängd tittar vi först på bivillkoret:

\[ h \, = \, \displaystyle {250 \over \pi\,r} \, - \, r \]

Av detta framgår att \( \; r \; \) inte får vara \( \, 0 \, \): \( \; r \, \neq \, 0 \; \).

Dessutom kan \( \; r \; \) som en längd inte vara negativ. Därför är \( \, 0 \, \) en undre gräns för \( \, r \, \):

\[ r \, > \, 0 \]

För att hitta en övre gräns (största möjliga värde) för \( \; r \; \) tittar vi på cylinderns begränsningsarea:

\[ \, A \, = \, 2\,\pi\,r\,h \, + 2\,\pi\,r^2 \, = \, 500 \]

Pga begränsningsareans konstanta värde \( \, 500 \, \) blir cylinderns radie störst när höjden blir \( \, 0 \, \).

Därför får vi radiens största värde \( \, r_{max} \, \) om vi i formeln ovan väljer \( \, h=0 \, \):

\[ \, h = 0 \qquad \Longrightarrow \qquad A \, = \, 2\,\pi \cdot \left(r_{max}\right)\,^2 \, = \, 500 \]

Varav följer:

\[ \, r_{max} \, = \, \sqrt{500 \over 2\,\pi} \, = \, 8,92 \]

Därmed blir målfunktionens definitionsmängd:

\( 0 \; < \; r \; \leq \; 8,92 \)

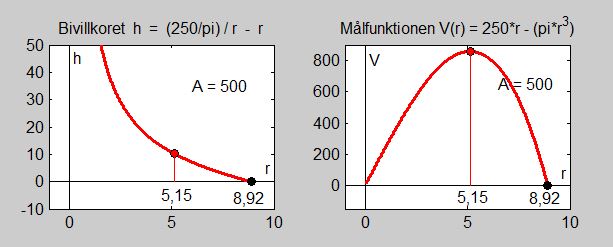
Grafen till vänster visar bivillkoret och grafen till höger målfunktionen, båda som funktioner av \( \, r \, \) med definitionsmängden ovan:

Målfunktionens graf visar att volymen blir maximal för \( \, r = 5,15 \, \).

Bivillkorets graf visar att \( \, r \, \) inte kan bli större än \( \, 8,92 \, \), medan \( \, h \, \) kan växa obegränsat när \( \, r \, \) går mot \( \, 0 \, \).

e) Resultaten från c) sätter vi in i målfunktionen för att få cylinderns största volym:

\[ V(5,15) \, = \, \pi \, \cdot 5,15^2 \, \cdot 10,30 \, = \, 858,23 \]

Konservburkens maximala volym blir \( \; 858,23 \, {\rm cm}^3 \; \).

f) Följande samband råder mellan cylinderns radie \( \; r = 5,15 \, {\rm cm} \; \) och dess höjd \( \; h = 10,30 \, {\rm cm} \; \) när volymen till en cylinder med en begränsningsarea på \( \, 500 \, {\rm cm}^2 \, \), maximeras:

\( 2 \; r \; = \; h \)

Återstår frågan om samma samband även råder generellt mellan radien \( \; r \; \) och höjden \( \; h \; \) för alla konservburkar med given begränsningsarea och maximal volym:

Diametern \( \; = \; \) Höjden

Denna fråga är föremål för undersökning i övning 9. En annan intressant frågeställning är:

Råder även samma samband \( \; 2 \, r \, = \, h \; \) om man utgår från en konservburk med fast given volym och istället minimerar materialåtgången för konservburken?

En närmare undersökning kommer att visa att detta är fallet.

Ett ekonomiskt exempel

Se övning 7.

@@ Rad 1: / Rad 1: @@
 {| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
 | style="border-bottom:1px solid #797979" width="5px" | &nbsp;
-{{Not selected tab|[[3.4 Kurvkonstruktioner|<-- Förra avsnitt]]}}
 {{Selected tab|[[3.5 Extremvärdesproblem|Genomgång]]}}
 {{Not selected tab|[[3.5 Övningar till Extremvärdesproblem|Övningar]]}}
 {{Not selected tab|[[Detta diagnosprov ingår inte i demon.|<span style="color:red">Diagnosprov kap 3 Anv. av deriv.</span>]]}}
-<!-- {{Not selected tab|[[Diagnosprov kap 3 Användning av derivata|Diagnosprov kap 3 Anv. av deriv.]]}} -->
 {{Not selected tab|[[Dessa lösningar ingår inte i demon.|<span style="color:red">Lösningar till diagnosprov kap 3</span>]]}}
-<!-- {{Not selected tab|[[Lösningar till diagnosprov kap 3 Användning av derivata|Lösningar till diagnosprov kap 3]]}} -->
 | style="border-bottom:1px solid #797979"  width="100%"| &nbsp;
 |}

Skillnad mellan versioner av "3.5 Extremvärdesproblem"

Versionen från 9 juni 2015 kl. 00.23

Exempel 1 Rektangel i parabel

Exempel 2 Glasskiva (rektangel i triangel)

Exempel 3 Konservburk

Ett ekonomiskt exempel

Navigeringsmeny

Personliga verktyg

Matematik 1b

Matematik 3c

Sök