Skillnad mellan versioner av "Ekvationer"

Versionen från 7 mars 2015 kl. 15.55

Teori

Innehåll

1 Olika typer av ekvationer
2 Rotbegreppet
3 Rotekvationer
- 3.1 Exempel
- 3.2 Den falska roten
4 4:e gradsekvationer med jämna x-potenser
5 Internetlänkar

Olika typer av ekvationer

Ekvationer har vi lärt oss ända från grundskolan till gymnasiet. I Matte 1-kursen har vi bl.a. löst ekvationer av följande typ.

Linjära ekvationer:

\[ 4\,x - (3\,x + 2) = -5\,x+12 \]

Sådana ekvationer kallas linjära eller 1:a gradsekvationer eftersom obekanten \( x\, \) förekommer endast som 1:a gradspotens dvs med exponenten 1. \( x\, \) är ju samma som \( x^1\, \). Högre \( \, x\)-potenser förekommer inte i ekvationen. I Matte 2-kursen har vi gått ett steg vidare och löst bl.a. ekvationer av följande typ:

Andragradsekvationer:

\[ x^2 + 6\,x - 16 = 0 \]

Sådana ekvationer kallas icke-linjära, närmare bestämt kvadratiska eller 2:a gradsekvationer därför att obekanten \( x\, \) förekommer högst som 2:a gradspotens dvs med exponenten 2 eller som \( x^2\, \). Obekantens exponent är alltså avgörande för ekvationens typ och därmed för svårighetsgraden när man vill lösa ekvationen. I Matte 2 har vi lärt oss att lösa 2:a gradsekvationer med följande metoder:

Nollproduktmeoden

Kvadratrotsmetoden

p-q-formeln:

Normalformen \(x^2 + p\,x + q = 0\,\) till en 2:a gradsekvation kan lösas med p-q formeln:

\[x_{1,2}=-\frac{p}{2}\pm\sqrt{\bigg(\frac{p}{2}\bigg)^2-q}\]

Vietas formler

Högre gradsekvationer:

Den generella lösningen av 3:e- och högre gradsekvationer är så pass svår att den inte behandlas i skolan. Det är t.o.m. principiellt omöjligt att med algebraiska operationer dvs \( + \), \( - \), \( \cdot \), \( / \) och \( {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} \) lösa ekvationer av 5:e och högre grad i generell form. Detta är en viktig sats inom algebran som bevisades av den norske matematikern Niels Henrik Abel så sent som 1824.

Sådana ekvationer som inte går att lösa algebraiskt, kan dock i praktiken lösas med numeriska metoder som man kan programmera och låta datorn göra jobbet. Vissa specialfall däremot går att lösa algebraiskt. Vi kommer att ta upp en speciell typ av 4:e gradsekvation som går att återföra till en 2:a gradsekvation.

Men först ska vi komplettera våra kunskaper om ekvationslösning med bl.a. ekvationer av en helt ny typ:

Rotekvationer:

\[ \sqrt{{\color{White}{[}}\!6\,x + 10} \, + \, 1 \, = \, x \]

Sådana ekvationer kallas rotekvationer. De är varken linjära eller kvadratiska. Med rot menar vi i hela detta avsnitt 2:a dvs kvadratroten. Vi kommer att lösa rotekvationer genom att återföra dem till 2:a gradsekvationer, precis som man återför 2:a gradsekvationer till 1:a gradsekvationer. Man bryter ned den nya, okända typen med stor svårighetsgrad till en lägre, redan känd typ med mindre svårighetsgrad.

Rotbegreppet

Innan vi ger oss på rotekvationer är det bra att komma ihåg vad rotdragning egentligen är för räkneoperation. Vill vi t.ex. lösa följande 2:a gradsekvationen måste vi dra roten ur bägge leden:

\[ x^2 = 4\; \]

På vänsterled blir det x därför att rotdragning tar ut kvadraten i vänsterledet eftersom de per definition är s.k. inversa (omvända) operationer, precis som paren addition/subtraktion och multiplikation/division. Men vad blir det på högerledet? Här måste vi precisera vårt rotbegrepp. Rotdragning ger alltid ett positivt värde som resultat:

\[ \qquad \sqrt{4}\;= 2\;, \quad {\rm inte}\;-2 \]

Detta säger inte emot att ekvationen \( x^2 = 4\, \) har två lösningar \( x_1 = 2\, \) och \( x_2 = -2\, \). Anldeningen till dessa två lösningar är dock INTE att \( \sqrt{4} \) kan vara \( -2\, \), för det är fel. \( \sqrt{4} \not= -2 \), utan \( \sqrt{4} = +2 \) och inget annat. Anldeningen till att ekvationen \( x^2 = 4\, \) ändå har både lösningen \( x_1 = 2\, \) och \( x_2 = -2\, \) är att båda dessa lösningar uppfyller ekvationen \( x^2 = 4\, \) dvs sätter man in dem i ekvationen blir vänsterled = högerled.

För att förstå detta måste vi tolka räkneoperationen \( {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} \) som en funktion, nämligen funktionen \( y = \sqrt{x} \). Funktionsbegreppet samt notationen \( y = f\,(x) \) tillåter nämligen inte två olika \( \, y\)-värden till ett \( \, x\)-värde. Vi påminner om funktionens definition från Matte 1-kursen:

Funktionsbegreppet:

En funktion \( y = f\,(x) \) är en föreskrift (formel, graf eller tabell) som tilldelar varje \( \,x\)-värde ENDAST ett \( \,y\)-värde.

Därför är \( \sqrt{4} = 2 \) och kan inte samtidigt vara \( -2\, \).

Rotens två olika betydelser:

Ordet rot har i matematiken olika betydelser i olika sammanhang:

Räkneoperationen rotdragning med rottecknet \( {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} \) som symbol, t.ex. roten ur \( 4\, \) är \( 2\, \) osv.

Lösningen av en ekvation. I ekvationssammanhang är rot synonym till en ekvations lösning. T.ex. är \( x_1 = 2\, \) och \( x_2 = -2\, \) rötter dvs lösningar till ekvationen \( x^2 = 4\, \).

Nollstället till ett polynom. I polynomsammanhang är rot synonym till ett polynoms nollställe. I exemplet ovan är \( x_1 = 2\, \) och \( x_2 = -2\, \) rötter dvs nollställen till polynomet \( x^2 - 4\, \).

Sammanhanget avgör vilken betydelse som gäller just i den aktuella kontexten. När vi nu i fortsättningen pratar om en rotekvations falska rötter menar vi falska lösningar.

Rotekvationer

Förekommer en ekvations obekant \(x\) under rotsymbolen \( {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} \) pratar man om en rotekvation. Sådana ekvationer löser man genom att isolera roten (som en faktor) på en sida av ekvationen och kvadrera sedan båda leden för att eliminera roten. Men här uppstår ett fenomen som är typiskt för rotekvationer: Kvadreringen kan generera s.k. falska rötter dvs falska lösningar och tillföra dem till ekvationen.

En rotekvation kan ha inga, en eller flera falska rötter. Vilka av de erhållna lösningarna är falska, kan man bara få reda på om man verifierar dem genom prövning, dvs man sätter in dem i den ursprungliga rotekvationen och prövar vilka som uppfyller rotekvationen. De falska rötterna är inte lösningar till rotekvationen utan till den kvadredade ekvationen och måste därför förkastas. Fenomenet med falska rötter beror på att kvadrering som är oundviklig för att eliminera \( {\color{White}{y=}}\!\!\!\!\!\!\!\!\sqrt{\color{White}x} \) genererar falska rötter. Men kvadrering är en operation vars inversa (omvända) operation (rotdragning) inte är entydig: 2 kvarderat ger 4, men även -2 kvarderat ger 4.

Nedanstående exempel, rotekvationen \( \sqrt{{\color{White}{[}}\!6\,x + 10} + 1 = x \) demonstrerar hur man kan lösa rotekvationer och identifiera samt eliminera falska rötter. I exemplet uppstår falska rötter så här:

Högerledet \( (x-1)\, \) på andra raden ger kvarderat \( (x-1)^2\, \). Men även \( -(x-1)\, \) skulle ge kvarderat \( (x-1)^2\, \). Däremot härstammer \( -(x-1)\, \) inte från den rotekvation vi vill lösa utan från en helt annan rotekvation, nämligen från \( \sqrt{{\color{White}{[}}\!6\,x + 10} - 1 = -x \). På så sätt smyger sig in en annan ekvations lösning i vår rotekvation. Därför kommer den att visa sig vara falsk.

Exempel

Första steget i att lösa en rotekvation är att skriva om den till en 2:a gradsekvation. För att göra det isolerar vi först roten på en sida av ekvationen genom att subtrahera 1 från bägge leden. Sedan kvadrerar vi bägge leden för att eliminera roten, för kvadrering är ju rotdragningens inversa operation. De tar ut varandra.

\[\begin{align} \sqrt{{\color{White}{[}}\!6\,x + 10} \, + \, 1 & = x & | \;\; -1 \\ \sqrt{{\color{White}{[}}\!6\,x + 10} & = x - 1 & | \; (\;\;\;)^2 \\ 6\,x + 10 & = (x - 1)^2 \\ 6\,x + 10 & = x^2 - 2 x + 1 \qquad\qquad & | - 10 \\ 6\,x & = x^2 - 2 x - 9 \qquad\qquad & | - 6 x \\ 0 & = x^2 - 8 x - 9 \\ \end{align}\]

Vi ser att rotekvationen leder till 2:a gradsekvationen ovan. Denna kan lösas bl.a. med p-q formeln där \( p = -8\, \) och \( q = -9\, \):

\[\begin{align} x^2 - 8\,x - 9 & = 0 \\ x_{1,2} & = 4 \pm \sqrt{{\color{White}{[}}\!16 + 9} \\ x_{1,2} & = 4 \pm 5 \\ x_1 & = 9 \\ x_2 & = - 1 \\ \end{align}\]

OBS! Dessa två lösningar är inte nödvändigtvis lösningar till den ursprungliga rotekvationen utan till:

\[ 6\,x + 10 = (x - 1)^2\, \]

Denna ekvation fick vi när vi kvadrerade rotekvationen ovan. Den ursprungliga rotekvationens lösningar är en del av denna kvadrerade ekvationen. Det kan däremot finnas lösningar här som inte löser rotekvationen, s.k. falska rötter.

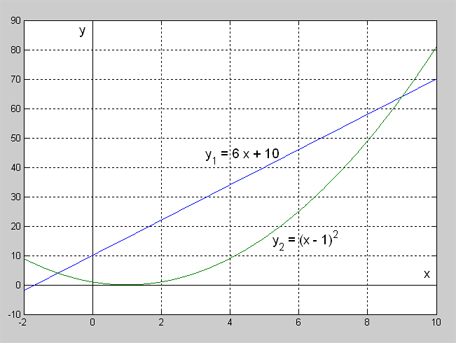
För att få en intuitiv uppfattning om falska rötter-fenomenet ritar vi graferna till funktionerna \( y_1 = 6 x + 10\, \) (vänsterledet i ekvationen ovan) och \( y_2 = (x - 1)^2\, \) (högerledet) i samma koordinatsystem:

Ekvationens lösningar kan avläsas från grafernas skärningspunkter vid \( x_1 = 9\, \) och \( x_2 = -1\, \).

Om de också är lösningar till rotekvationen måste undersökas algebraiskt:

Den falska roten

Andra steget i att lösa rotekvationen

\[ \sqrt{{\color{White}{[}}\!6\,x + 10} \, + \, 1 \, = \, x \]

är att identifiera falska rötter (lösningar). Observera att detta steg är ett obligatoriskt moment vid lösningen av rotekvationer. Vilken av lösningarna ovan är den falska roten? Eller är kanske båda falska eller ingen av dem? Teoretiskt kan alla, några eller ingen av rotekvationens rötter vara falska. Enda kriteriet är om de uppfyller den ursprungliga rotekvationen eller ej. Därför måste vi pröva vi båda.

Först prövar vi roten \( x_1 = 9\, \):

Vänsterled (VL) \( {\color{White} x} \sqrt{{\color{White}{|}}\!6 \cdot 9 + 10} + 1 = \sqrt{{\color{White}{|}}\!54 + 10} + 1 = \sqrt{{\color{White}{|}} 64} + 1 = 8 + 1 = 9 \)

Högerled (HL) \( {\color{White} x} 9 \, \)

VL = HL \( \Rightarrow\; x_1 = 9 \) är en sann rot.

Sedan prövar vi roten \( x_2 = -1\, \):

Vänsterled (VL) \( {\color{White} x} \sqrt{{\color{White}{|}}\!6 \cdot (-1) + 10} + 1 = \sqrt{{\color{White}{|}}\!-6 + 10} + 1 = \sqrt{4} + 1 = 2 + 1 = 3 \)

Högerled (HL) \( {\color{White} x} -1 \, \)

VL \( \not= \) HL \( \Rightarrow\; x_2 = -1 \) är en falsk rot.

Slutligen kan vi konstatera att vår rotekvation

\[ \sqrt{{\color{White}{[}}\!6\,x + 10} \; + \; 1 \; = \; x \]

har den enda lösningen:

\[ x = 9\, \]

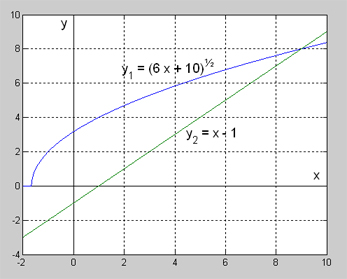
För att även här få en intuitiv uppfattning om lösningarna till den den ursprungliga rotekvationen ritar vi graferna till funktionerna \( y_1 = \sqrt{{\color{White}{[}}\!6\,x + 10} \;\;\big(\)samma som \( y_1 = (6 x + 10)^{1 \over 2} \) enligt potenslagarna \(\big)\) och \( y_2 = x - 1\, \) i samma koordinatsystem:

Rotekvationens lösning kan avläsas från grafernas skärningspunkt vid \( x = 9\, \).

Rotekvationer kan även lösas med andra metoder som vi inte tar upp här. En av dem är substitution, även kallad variabelbyte. Från Matte B-kursens linjära ekvationssystem vet vi att substitution betyder ersättning av en variabel med ett uttryck av en annan variabel. I övning 7 finns ett exempel på denna metod för rotekvationer. Substitution används nästan alltid när man vill lösa 4:e gradsekvationer som vi behandlar nu.

4:e gradsekvationer med jämna x-potenser

Inledningsvis sa vi att vissa specialfall av högre gradsekvationer går att lösa algebraiskt. Vi ska nu ta upp en speciell typ av 4:e gradsekvation som går att återföra till en 2:a gradsekvation. Denna speciella typ utmärker sig genom att obekanten \( x \) endast förekommer i potenser med jämna exponenter dvs med exponenterna 4, 2 och 0. Dvs ekvationen saknar helt och hållet termer med udda x-potenser. Följande är ett exempel på en sådan 4:e gradsekvation med jämna x-potenser:

\[ x^4 - 6\,x^2 - 27 = 0 \]

En 4:e gradsekvation med jämna x-potenser kan alltid skrivas om till en 2:a gradsekvation genom en enkel substitution dvs ett variabelbyte. Vi inför en ny variabel z som vi definierar som:

\[ \displaystyle z = x^2 \]

Läs nu denna substitution från höger, så här: Ersätt \( x^2 \) med \( z \) dvs sätt in i 4:e gradsekvationen ovan \( z \) istället för \( x^2 \). Denna substitution överför 4:e gradsekvationen till en 2:a gradsekvation:

\[\begin{align} (x^2)^2 - 6\,(x^2) - 27 & = 0 \\ z^2 - 6\,z - 27 & = 0 \\ \end{align}\]

Självklart är detta en ny ekvation med den nya obekanten z. Men den är relaterad till vår ursprungliga 4:e gradsekvation via substitutionen \( z = x^2 \) som i sin tur kan anses som en liten ekvation. Dvs 2:a gradsekvationens z-lösningar insatta i substitutionsekvationen ger x-lösningar till den ursprungliga 4:e gradsekvationen. Därför behöver vi bara lösa den nya 2:a gradsekvationen och sätta in dess z-lösningar i substitutionen för att få x-lösningar för den ursprungliga 4:e gradsekvationen. Så här går det till:

\[\begin{align} z^2 - 6\,z - 27 & = 0 \\ z_{1,2} & = 3 \pm \sqrt{9 + 27} \\ z_{1,2} & = 3 \pm 6 \\ z_1 & = 9 \\ z_2 & = - 3 \\ \end{align}\]

Övergången från z till x gör vi genom att först sätta in lösningen \( z_1 = 9 \) i substitutionen \( z = x^2 \):

\[ \displaystyle z = x^2 = 9 \]

Nu drar vi roten ur båda leden i ekvationen \( x^2 = 9 \) och får lösningarna:

\[ x_{1,2} = \pm 3 \]

Sedan görs samma sak med lösningen \( z_2 = -3 \). Insatt i substitutionen \( z = x^2 \) ger den:

\[ \displaystyle z = x^2 = -3 \]

Men ekvationen \( x^2 = -3 \) har inga lösningar pga att roten \( \sqrt{-3} \) ur ett negativt tal inte är definierad.

Slutligen kan vi sammanfatta och konstatera att vår 4:e gradsekvation

\[ x^4 - 6\,x^2 - 27 = 0 \]

har de två lösningarna:

\[\begin{align} x_1 & = 3 \\ x_2 & = - 3 \\ \end{align}\]

En prövning bekräftar detta resultat.

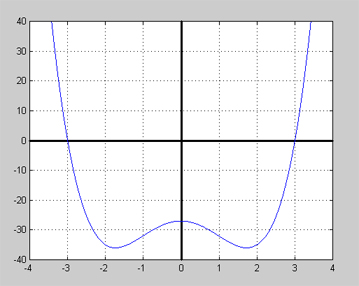
Så här ser grafen till funktionen \( y = x^4 - 6\,x^2 - 27 \) ut vars nollställen överensstämmer med våra lösningar:

Internetlänkar

http://www.youtube.com/watch?v=V8I2_zgNRHI

http://www.matteguiden.se/matte-c/polynomfunktioner/andra-typer-av-ekvationer/#Rotekvationer

http://www.pluggakuten.se/wiki/index.php?title=Rotekvation

http://wiki.math.se/wikis/forberedandematte1/index.php/3.2_Rotekvationer

http://wiki.math.se/wikis/sf0600_0701/index.php/3.2_Rotekvationer

Versionen från 7 mars 2015 kl. 15.44 (visa wikitext) Taifun (Diskussion \| bidrag) m ← Äldre redigering		Versionen från 7 mars 2015 kl. 15.55 (visa wikitext) Taifun (Diskussion \| bidrag) m Nyare redigering →
Rad 259:		Rad 259:

	http://wiki.math.se/wikis/sf0600_0701/index.php/3.2_Rotekvationer		http://wiki.math.se/wikis/sf0600_0701/index.php/3.2_Rotekvationer
		+
		+
		+
		+
		+



	[[Matte:Copyrights\|Copyright]] © 2011-2015 Taifun Alishenas. All Rights Reserved.		[[Matte:Copyrights\|Copyright]] © 2011-2015 Taifun Alishenas. All Rights Reserved.