Skillnad mellan versioner av "3.5 Extremvärdesproblem"
Från Mathonline
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 9: | Rad 9: | ||
| − | [[Media: Lektion 33 Extremvärdesproblem Ruta.pdf|Lektion 33 Extremvärdesproblem]] | + | [[Media: Lektion 33 Extremvärdesproblem I Ruta.pdf|Lektion 33 Extremvärdesproblem I]] |
| + | |||
| + | [[Media: Lektion 34 Extremvärdesproblem II Ruta.pdf|Lektion 34 Extremvärdesproblem II]] | ||
__TOC__ | __TOC__ | ||
| Rad 16: | Rad 18: | ||
== Exempel 1 Glasskiva == | == Exempel 1 Glasskiva == | ||
| − | En | + | En glasskiva har formen av en rätvinklig triangel med följande mått i cm: |
| + | |||
| + | :::[[Image: Ovn 3_2_10_40.jpg]] | ||
| + | Ur skivan ska en rektangulär glasplatta skäras ut så att glasplattans area <math> \, A(x) \, </math> blir maximal. | ||
a) Ställ upp en funktion som beskriver priset <math> y \, </math> i kr som en funktion av antalet <math> n \, </math> sålda ägg. | a) Ställ upp en funktion som beskriver priset <math> y \, </math> i kr som en funktion av antalet <math> n \, </math> sålda ägg. | ||
Versionen från 25 januari 2015 kl. 13.05
| <-- Förra avsnitt | Teori | Övningar | --> Nästa avsnitt |
Lektion 33 Extremvärdesproblem I
Lektion 34 Extremvärdesproblem II
Innehåll
Exempel 1 Glasskiva
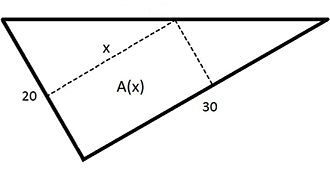
En glasskiva har formen av en rätvinklig triangel med följande mått i cm:
Ur skivan ska en rektangulär glasplatta skäras ut så att glasplattans area \( \, A(x) \, \) blir maximal.
a) Ställ upp en funktion som beskriver priset \( y \, \) i kr som en funktion av antalet \( n \, \) sålda ägg.
b) Rita grafen till prisfunktionen från a).
Lösning:
a) \( {\color{White} x} {\color{Red} 1} \, \) ägg kostar \( {\color{Red} 1} \cdot 3 \;{\rm kr,} \)