Skillnad mellan versioner av "1.3 Polynom i faktorform"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m (→Det allmänna fallet (icke-normalform)) |
||
| Rad 189: | Rad 189: | ||
::::::::::<math> 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-3) \cdot (x+1) </math> | ::::::::::<math> 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-3) \cdot (x+1) </math> | ||
| − | Den ovan beskrivna metoden fungerar alltid när | + | Den ovan beskrivna metoden fungerar alltid när 2:a gradspolynomet har ett eller två nollställen. Har det däremot inget nollställe alls finns det inte heller någon faktorisering. |
== Faktorisering av 3:e och högre gradspolynom == | == Faktorisering av 3:e och högre gradspolynom == | ||
Versionen från 1 januari 2011 kl. 16.35
| Teori | Övningar |
Innehåll
Vad är en faktor?
Du minns väl att ett uttryck av formen
- \[ a \cdot b \]
är en produkt. Ingredienserna \(a\) och \(b\) kallas faktorer. Så länge \(a\) och \(b\) är tal är uttrycket ovan en faktorisering av tal. T.ex. är 3 \(\cdot\) 4 en faktorisering av 12.
En faktorisering av polynom innebär att skriva om polynomet, som ursprungligen är en summa av termer, till en produkt. T.ex.:
- \[ x^2 - 7\,x + 12 = (x-3) \cdot (x-4) \]
Till vänster om likhetstecknet har vi ett vanligt polynom. Till höger står en produkt som kallas polynom i faktorform som är resultat av faktorisering. Ingredienserna i faktorformen dvs faktorerna \( (x-3)\, \) och \( (x-4)\, \) är i sin tur polynom, fast av mindre grad, nämligen 1. Ursprungspolynomet är av grad 2, liknande faktorerna 3 och 4 som är mindre än 12.
Likheten ovan mellan polynomet och dess faktorform inser man genom att utveckla produkten:
- \[ (x-3) \cdot (x-4) = x^2 - 4\,x - 3\,x + 3 \cdot 4 = x^2 - 7\,x + 12 \]
Men hur får man fram faktorformen från polynomet? Eller: Hur faktoriserar man ett polynom?
Faktorisering av 2:a gradspolynom
Sätter man polynomet \( x^2 - 7\,x + 12 \) till 0 uppstår ekvationen:
- \[ x^2 - 7\,x + 12 = (x-3) \cdot (x-4) = 0 \]
En ekvation innebär att hitta de tal x för vilka ekvationen gäller. Därför är denna ekvations lösningar polynomets nollställen, dvs de tal x för vilka polynomets värden blir 0. Polynomets faktorform \((x-3) (x-4) \) tillåter oss att med nollproduktmetoden hitta lösningarna till ekvationen ovan utan att räkna. Nollproduktmetoden viar nämligen att 3 och 4 är lösningar till ekvationen \( (x-3) (x-4) = 0 \): För att produkten \( (x-3) (x-4) \) ska vara lika med 0 måste antingen den första faktorn \( (x-3) \) eller den andra faktorn \( (x-4) \) vara lika med 0. För att \( (x-3) \) eller \( (x-4) \) ska vara lika med 0 måste \( x \) antingen vara lika med 3 eller lika med 4. Detta i sin tur innebär att 3 och 4 är lösningar till ekvationen \( (x-3) (x-4) = 0 \). Pga likheten mellan polynom och dess faktorform måste 3 och 4 även vara polynomets nollställen dvs lösningar till ekvationen ovan.
Resonemanget ovan ger oss nu en metod i handen for att få fram faktorformen från polynomet. För att faktorisera polynomet\( x^2 - 7\,x + 12 \) behöver vi bara beräkna dess nollställen, säg x1 och x2, och sedan skriva upp faktorformen \((x-x1) (x-x2) \). Låt oss genomföra det i vårt exempel:
- \[\begin{align} x^2 - 7\,x + 12 & = 0 \\ x_{1,2} & = 3,5 \pm \sqrt{12,25 - 12} \\ x_{1,2} & = 3,5 \pm \sqrt{0,25} \\ x_{1,2} & = 3,5 \pm 0,5 \\ x_1 & = 4 \\ x_2 & = 3 \\ \end{align}\]
Därför har polynomet \( x^2 - 7\,x + 12 \) faktorformen \( (x-3) \cdot (x-4) \). Vi kommer att lära oss en effektivare metod för lösning av 2:a gradsekvationer och därmed för faktorisering av 2:gradspolynom, när vi lärt oss ett enkelt samband mellan ett polynoms koefficienter och dess nollställen.
Det som vi genomförde för vårt exempel kan generaliseras till alla 2:gradspolynom (i normalform):
Sats (Faktorisering 2 nollställen):
- Om 2:gradspolynomet \( x^2 + p\,x + q \) har nollställena \( x_1\, \) och \( x_2\, \) så gäller:
- \[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) \]
För att bevisa satsen ovan kan man t.ex. sätta in 2:a gradsekvationens lösningsformel (pq-formeln) för \( x_1\, \) och \( x_2\, \) och utveckla produkten på högerledet. En jämförelse av koefficienter kommer att resultera i likhet med vänsterledet. Det finns motsvarande satser om polynom av högre grad än 2 som vi inte behandlar här.
Istället ska vi undersöka ett enkelt, men intressant samband mellan 2:a gradspolynomets koefficienter \( p\, \) och \( q\, \) och dess nollställen \( x_1\, \) och \( x_2\, \), vilket ger dig möjligheten att roa dina vänner genom att låta dem säga två tal, t.ex. 3 och 4, och omedelbart skriva upp den 2:a gradsekvation vars lösningar just är 3 och 4.
Samband mellan koefficienter och nollställen
Vi åter anknyter till likheten mellan polynom och dess faktorform som vi behandlade ovan (Faktorisering av 2: gradspolynom) genom att utveckla produkten:
- \[ (x-3) \cdot (x-4) = x^2 - 4\,x - 3\,x + 3 \cdot 4 = x^2 - (3+4)\,x + 3 \cdot 4 = x^2 - 7\,x + 12 \]
Att vi i mellanräkningen, till synes onödigt, skriver \( x^2 - (3+4)\,x + 3 \cdot 4 \) beror på att vi vill förtydliga sambandet mellan polynomets koefficienter -7 och 12 å ena sidan och dess nollställen 3 och 4 å andra sidan: x-termens koefficient -7 är summan av 3 och 4 med omvänt förtecken. Polynomets konstanta term 12 är produkten till 3 och 4, dvs:
- \[ 3 + 4 = 7 \qquad {\rm och} \qquad 3 \cdot 4 = 12 \]
På så sätt kan du roa dina vänner genom att låta dem säga två tal, t.ex. 3 och 4, och omedelbart skriva upp 2:a gradsekvationen
- \[ x^2 - 7\,x + 12 = 0 \]
och låta dina vänner lösa ekvationen. De kommer att få just dessa två tal som lösningar. För att bilda ekvationen behöver du bara summera talen och sätta summan med omvänt förtecken framför x samt multiplicera talen med varandra och använda produkten som 2:a gradsekvationens konstanta term. Prova gärna med andra tal. Det kommer alltid att stämma, vilket inte är något trolleri utan resultat av följande generell matematisk sats:
Sats (Vietas formler):
- Om 2:gradspolynomet \( x^2 + p\,x + q \) har nollställena \( x_1\, \) och \( x_2\, \) så gäller:
- \[ x_1 + x_2 = -p \qquad {\rm och} \qquad x_1 \cdot x_2 = q \]
Bevis:
Genom att använda satsen som vi formulerade i slutet av förra paragrafen (Faktorisering 2 nollställen) kan vi skriva:
- \[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) \]
Om vi nu utvecklar produkten på höger sidan kan vi skriva vidare:
- \[ x^2 + p\,x + q = (x-x_1) \cdot (x-x_2) = x^2 - x_2\,x - x_1\,x + x_1 \cdot x_2 = x^2 - (x_1+x_2)\,x + x_1 \cdot x_2 \]
En jämförelse av koefficienterna mellan polynomet \( x^2 - (x_1+x_2)\,x + x_1 \cdot x_2 \) (högerledet) och polynomet \( x^2 + p\,x + q \) (vänsterledet) ger resultatet:
- \[ x_1 + x_2 = -p \qquad {\rm och} \qquad x_1 \cdot x_2 = q \]
Vad som skulle bevisas (V.s.b.).
Även denna sats kan generaliseras till polynom av högre grad än 2. Den franske matematikern François Viète|(1540-1603) var en av de första som såg sambandet mellan ett polynoms koefficienter och dess nollställen. Därför kallas formlerna \( x_1 + x_2 = -p\, \) och \( x_1 \cdot x_2 = q \) efter honom Vietas formler.
Er stor fördel av Vietas formler för oss är att man kan lösa 2:a gradsekvationer och därmed faktorisera polynom utan att behöva använda lösningsformeln. Detta innebär mindre räknearbete vilket i sin tur minskar risken för felräkning. På köpet går det fortare att ta fram polynomens faktorform.
Exempel 1
Ta ekvationen
\( x^2 - 7\,x + 10 = 0 \)
För lösningarna \( x_1\,\) och \( x_2\,\) måste enligt Vietas formler gälla\[ \begin{align} x_1 + x_2 & = -(-7) = 7 \\ x_1 \cdot x_2 & = 10 \end{align}\]
Vi måste alltså hitta två tal vars produkt är 10 och vars summa är 7. Med lite provande hittar man 2 und 5 eftersom \( 2 + 5 = 7\, \) och \( 2 \cdot 5 = 10 \). Prövning bekräftar resultatet.
Har vi på det här enkla sättet hittat nollställena till polynomet \( x^2 - 7\,x + 10 \) kan vi skriva upp faktorformen\[ x^2 - 7\,x + 10 = (x - 2) \cdot (x - 5) \]
Utveckling av produkten på höger sidan bekräftar faktoriseringen.
Exempel 2
Till ekvationen
\( x^2 - 6\,x + 9 = 0 \)
ger Vietas formler\[ \begin{align} x_1 + x_2 & = -(-6) = 6 \\ x_1 \cdot x_2 & = 9 \end{align}\]
Man hittar lösningarna \( x_1 = 3\,\) och \( x_2 = 3\,\) eftersom \( 3 + 3 = 6\,\) och \( 3 \cdot 3 = 9 \).
Därför kan polynomet \( x^2 - 6\,x + 9 \) faktoriseras så här\[ x^2 - 6\,x + 9 = (x - 3) \cdot (x - 3) = (x - 3)^2 \]
Det intressanta med detta exempel är att vi endast har en lösning x = 3 till 2:a gradsekvationen \( x^2 - 6 x + 9 = 0 \). Fast, om vi tittar på faktorformen \( (x - 3) (x - 3) = 0 \) kan man lika bra säga att vi har två identiska lösningar - en filosofisk skillnad som man matematiskt brukar lösa upp genom att kalla lösningen för en dubbelrot till ekvationen.
Dubbelrot
Sats (Faktorisering 1 nollställe):
- Om 2:gradspolynomet \( x^2 + p\,x + q \) endast har ett nollställe \( x_1\, \) så gäller:
- \[ x^2 + p\,x + q = (x-x_1)^2 \]
- Ett sådant nollställe kallas för dubbelrot till ekvationen \( x^2 + p\,x + q = 0 \).
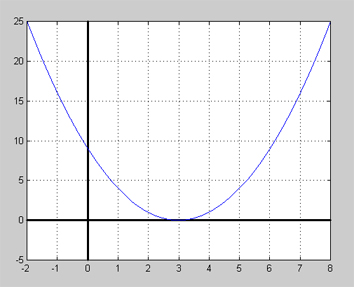
Dubbelrötter har vissa intressanta egenskaper. Låt oss börja att upptäcka dem genom att rita grafen till polynomfunktionen och undersöka på vilket sätt dubbelroten "skär" x-axeln. Vi tar polynomet från Exempel 2 ovan där ekvationen \( x^2 - 6\,x + 9 = 0 \) hade dubbelroten x = 3.
Så här ser grafen ut till polynomfunktionen \( y = x^2 - 6\,x + 9 \):
Grafen visar att kurvan inte skär utan bara berör x-axeln vid x = 3. Det är en av de typiska egenskaperna hos dubbelrötter. De ligger på gränsen mellan att skära (två lösningar) och inte skära x-axeln (ingen lösning alls). Matematiskt uttrycker sig denna egenskap i faktoriseringens form:
- \[ x^2 - 6\,x + 9 = (x-3) \cdot (x-3) = (x-3)^2 \]
Den dubbla förekomsten av faktorn (x-3) ger roten dess namn dubbelrot.
Det allmänna fallet (icke-normalform)
Alla våra hittills behandlade polynom var i normalform, dvs den ledande koefficienten (kvadratiska termens koefficient eller talet framför x²) var alltid 1. Det behöver inte alltid vara så. Låt oss t.ex. faktorisera följande polynom med ledande koefficienten 3:
- \[ 3\,x^2 - 6\,x - 9 \]
Lösningen består i att återföra problemet till den kända typen i normalform genom att bryta ut den ledande koefficienten:
- \[ 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-x_1) \cdot (x-x_2) \]
där \((x-x_1) \cdot (x-x_2)\) är faktoriseringen av polynomet \( x^2 - 2\,x - 3 \). Efter att ha löst detta nya problem kan vi komma tillbaka och sätta in lösningen i ansatsen ovan för att få faktoriseringen av \( 3\,x^2 - 6\,x - 9 \).
För att få fram \( x_1\,\) och \( x_2\,\) som ger oss faktoriseringen av \( x^2 - 2\,x - 3 \) kan vi som vanligt använda Vietas formler\[ \begin{align} x_1 + x_2 & = -(-2) = 2 \\ x_1 \cdot x_2 & = -3 \end{align}\]
Man hittar lösningarna \( x_1 = 3\,\) och \( x_2 = -1\,\) eftersom \( 3 + (-1) = 2\,\) och \( 3 \cdot (-1) = -3 \).
Därför kan polynomet \( x^2 - 2\,x - 3 \) faktoriseras så här\[ x^2 - 2\,x - 3 = (x - 3) \cdot (x + 1) \]
Går vi tillbaka och sätter in denna lösning i det ursprungliga problemets ansats får vi det det ursprungliga polynomets faktorisering:
- \[ 3\,x^2 - 6\,x - 9 = 3\,(x^2 - 2\,x - 3) = 3\,(x-3) \cdot (x+1) \]
Den ovan beskrivna metoden fungerar alltid när 2:a gradspolynomet har ett eller två nollställen. Har det däremot inget nollställe alls finns det inte heller någon faktorisering.