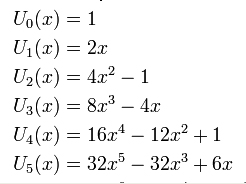Skillnad mellan versioner av "1.1 Fördjupning till Polynom"
Taifun (Diskussion | bidrag) m |
Taifun (Diskussion | bidrag) m |
||
| Rad 51: | Rad 51: | ||
Här följer graferna till polynomen ovan ritade i samma koordinatsystem. De visar att kurvorna svänger oftare och får fler maxima/minima ju högre deras grad är: | Här följer graferna till polynomen ovan ritade i samma koordinatsystem. De visar att kurvorna svänger oftare och får fler maxima/minima ju högre deras grad är: | ||
| − | [[Image: Chebyshev_Polyn_2nd_60.jpg]] | + | :[[Image: Chebyshev_Polyn_2nd_60.jpg]] |
Dessa polynom heter [http://mathworld.wolfram.com/ChebyshevPolynomialoftheSecondKind.html Chebyshevpolynom av 2:a slag] efter den ryske matematikern [http://en.wikipedia.org/wiki/Pafnuty_Chebyshev Chebyshev] som presenterade dem 1854. De är relaterade till varandra med följande formel, kallad <span style="color:red">rekursionsformel</span>: | Dessa polynom heter [http://mathworld.wolfram.com/ChebyshevPolynomialoftheSecondKind.html Chebyshevpolynom av 2:a slag] efter den ryske matematikern [http://en.wikipedia.org/wiki/Pafnuty_Chebyshev Chebyshev] som presenterade dem 1854. De är relaterade till varandra med följande formel, kallad <span style="color:red">rekursionsformel</span>: | ||
| − | + | ::<math> U_n(x) = 2\,x\,\cdot\,U_{n-1}(x)\,-\,U_{n-2}(x) \qquad\qquad n = 2, 3, ... </math> | |
| − | + | ::<math> U_0(x) = 1, \quad U_1(x) = 2\,x </math> | |
Denna formel ger oss möjligheten att ta fram Chebyshevpolynomen rekursivt (successivt), dvs vi kan ställa upp ett polynom med hjälp av de två föregående. De första två Chebyshevpolynomen <math>U_0, U_1\,</math> är explicit angivna (i den andra raden). Det tredje Chebyshevpolynomet <math>U_2\,</math> får man genom att sätta in <math>U_0, U_1\,</math> i högerledet av rekursionsformeln (i den första raden). Det fjärde Chebyshevpolynomet <math>U_3\,</math> får man genom att sätta in <math>U_1, U_2\,</math> i högerledet osv. Det finns oändligt många Chebyshevpolynom. I princip kan man få dem alla med rekursionsformeln utgående från de två första. Man kan säga att följden av Chebyshevpolynomen definieras och genereras av rekursionsformeln ovan. Låt oss börja med att ställa upp det tredje (OBS! n = 2) med hjälp av de två första (n = 0 och 1): | Denna formel ger oss möjligheten att ta fram Chebyshevpolynomen rekursivt (successivt), dvs vi kan ställa upp ett polynom med hjälp av de två föregående. De första två Chebyshevpolynomen <math>U_0, U_1\,</math> är explicit angivna (i den andra raden). Det tredje Chebyshevpolynomet <math>U_2\,</math> får man genom att sätta in <math>U_0, U_1\,</math> i högerledet av rekursionsformeln (i den första raden). Det fjärde Chebyshevpolynomet <math>U_3\,</math> får man genom att sätta in <math>U_1, U_2\,</math> i högerledet osv. Det finns oändligt många Chebyshevpolynom. I princip kan man få dem alla med rekursionsformeln utgående från de två första. Man kan säga att följden av Chebyshevpolynomen definieras och genereras av rekursionsformeln ovan. Låt oss börja med att ställa upp det tredje (OBS! n = 2) med hjälp av de två första (n = 0 och 1): | ||
| − | <math> \displaystyle U_0(x) = \underline{1} </math> | + | ::<math> \displaystyle U_0(x) = \underline{1} </math> |
| − | <math> U_1(x) = \underline{2\,x} </math> | + | ::<math> U_1(x) = \underline{2\,x} </math> |
För n = 2 ger rekursionsformeln: | För n = 2 ger rekursionsformeln: | ||
| − | <math> U_2(x) = 2\,x\,\cdot\,U_1(x)\,-\,U_0(x) = 2\,x\,\cdot\,2\,x\,-\,1 = \underline{4\,x^2\,-\,1} </math> | + | ::<math> U_2(x) = 2\,x\,\cdot\,U_1(x)\,-\,U_0(x) = 2\,x\,\cdot\,2\,x\,-\,1 = \underline{4\,x^2\,-\,1} </math> |
Sedan kan vi få fram <math> U_3(x) </math> genom att att sätta in n = 3 i rekursionsformeln: | Sedan kan vi få fram <math> U_3(x) </math> genom att att sätta in n = 3 i rekursionsformeln: | ||
| − | <math> U_3(x) = 2\,x\,\cdot\;U_2(x)\,-\,U_1(x) = 2\,x\,\cdot\,(4\,x^2\,-\,1)\,-\,2\,x = 8\,x^3\,-\,2\,x\,-\,2\,x = \underline{8\,x^3\,-\,4\,x} </math> | + | ::<math> U_3(x) = 2\,x\,\cdot\;U_2(x)\,-\,U_1(x) = 2\,x\,\cdot\,(4\,x^2\,-\,1)\,-\,2\,x = 8\,x^3\,-\,2\,x\,-\,2\,x = \underline{8\,x^3\,-\,4\,x} </math> |
För n = 4 ger rekursionsformeln <math> U_4(x) </math> osv.: | För n = 4 ger rekursionsformeln <math> U_4(x) </math> osv.: | ||
| − | <math> U_4(x) = 2\,x\,\cdot\,U_3(x)\,-\,U_2(x) = 2\,x\,\cdot\,(8\,x^3\,-\,4\,x)\,-\,(4\,x^2\,-\,1) = 16\,x^4\,-\,8\,x^2\,-\,4\,x^2\,+\,1 = \underline{16\,x^4\,-\,12\,x^2\,+\,1} </math> | + | ::<math> U_4(x) = 2\,x\,\cdot\,U_3(x)\,-\,U_2(x) = 2\,x\,\cdot\,(8\,x^3\,-\,4\,x)\,-\,(4\,x^2\,-\,1) = 16\,x^4\,-\,8\,x^2\,-\,4\,x^2\,+\,1 = \underline{16\,x^4\,-\,12\,x^2\,+\,1} </math> |
Så här kan man fortsätta för att få fram alla Chebyshevpolynom. Förfarandet är rekursivt eftersom formeln används för att ställa upp ett polynom från de två föregående. | Så här kan man fortsätta för att få fram alla Chebyshevpolynom. Förfarandet är rekursivt eftersom formeln används för att ställa upp ett polynom från de två föregående. | ||
| + | |||
== Jämförelse av koefficienter == | == Jämförelse av koefficienter == | ||
| Rad 90: | Rad 91: | ||
<span style="color:red">Två polynom</span>: | <span style="color:red">Två polynom</span>: | ||
| − | + | ::<math> P(x) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0 </math> | |
och | och | ||
| − | + | ::<math> Q(x) = b_n \cdot x^n + b_{n-1} \cdot x^{n-1} + \quad \ldots \quad + b_1 \cdot x + b_0 </math> | |
<span style="color:red">är lika med varandra</span> om de har samma grad och om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer, närmare bestämt om: | <span style="color:red">är lika med varandra</span> om de har samma grad och om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer, närmare bestämt om: | ||
| − | + | ::<math> a_n = b_n, \quad a_{n-1} = b_{n-1}, \quad \ldots \quad a_1 = b_1, \quad a_0 = b_0 </math> | |
---- | ---- | ||
| + | |||
===== Exempel 1 ===== | ===== Exempel 1 ===== | ||
| Rad 105: | Rad 107: | ||
Två polynom är givna: | Två polynom är givna: | ||
| − | : <math> P(x) = a \cdot x + 2\,a + b </math> | + | ::<math> P(x) = a \cdot x + 2\,a + b </math> |
| − | : <math> Q(x) = 2\,x + 1\!\, </math>. | + | ::<math> Q(x) = 2\,x + 1\!\, </math>. |
Låt <math> a\, </math> och <math> b\, </math> vara konstanter medan <math> x\, </math> är polynomens oberoende variabel. | Låt <math> a\, </math> och <math> b\, </math> vara konstanter medan <math> x\, </math> är polynomens oberoende variabel. | ||
| Rad 115: | Rad 117: | ||
Vi skriver <math> P(x),\, </math> och <math> Q(x)\, </math> så att vi lättare kan se motsvarande koefficienter: | Vi skriver <math> P(x),\, </math> och <math> Q(x)\, </math> så att vi lättare kan se motsvarande koefficienter: | ||
| − | : <math> P(x) = a \cdot x^1 + (2\,a + b) \cdot x^0 </math> | + | ::<math> P(x) = a \cdot x^1 + (2\,a + b) \cdot x^0 </math> |
| − | : <math> Q(x) = 2 \cdot x^1 + \quad\;\; 1 \quad\;\; \cdot x^0 </math> | + | ::<math> Q(x) = 2 \cdot x^1 + \quad\;\; 1 \quad\;\; \cdot x^0 </math> |
Jämförelse av koefficienterna till <math> x^1\, </math> leder till: | Jämförelse av koefficienterna till <math> x^1\, </math> leder till: | ||
| − | : <math> a = 2\,</math> | + | ::<math> a = 2\,</math> |
Jämförelse av koefficienterna till <math> x^0 \,</math> leder till: | Jämförelse av koefficienterna till <math> x^0 \,</math> leder till: | ||
| − | : <math> 2\,a + b = 1\!\,</math> | + | ::<math> 2\,a + b = 1\!\,</math> |
Sätter man in <math> a = 2\, </math> i denna relation får man <math> b = -3\, </math>. | Sätter man in <math> a = 2\, </math> i denna relation får man <math> b = -3\, </math>. | ||
| Rad 131: | Rad 133: | ||
Polynomen <math> P(x)\, </math> och <math> Q(x)\, </math> är lika med varandra för: | Polynomen <math> P(x)\, </math> och <math> Q(x)\, </math> är lika med varandra för: | ||
| − | : <math> a = 2\, </math> | + | ::<math> a = 2\, </math> |
| + | |||
| + | ::<math> b = -3\, </math> | ||
| − | |||
===== Exempel 2 ===== | ===== Exempel 2 ===== | ||
| Rad 141: | Rad 144: | ||
Hitta ett 2:a gradspolynom <math> Q(x)\, </math> så att: | Hitta ett 2:a gradspolynom <math> Q(x)\, </math> så att: | ||
| − | : <math> Q(x)\cdot (x-2) = P(x) </math> | + | ::<math> Q(x)\cdot (x-2) = P(x) </math> |
'''Svar:''' | '''Svar:''' | ||
| − | : <math> Q(x) = x^2 + 6 \, x + 13 </math> | + | ::<math> Q(x) = x^2 + 6 \, x + 13 </math> |
'''Lösning:''' | '''Lösning:''' | ||
| Rad 153: | Rad 156: | ||
Vi bestämmer koefficienterna <math> a\, , \, b\, </math> och <math> c\, </math> så att <math> Q(x)\cdot (x-2) = P(x) </math> | Vi bestämmer koefficienterna <math> a\, , \, b\, </math> och <math> c\, </math> så att <math> Q(x)\cdot (x-2) = P(x) </math> | ||
| − | <math>\begin{align} Q(x) \cdot (x - 2) & = (a\,x^2 + b\,x + c)\cdot (x - 2) = a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c = \\ | + | ::<math>\begin{align} Q(x) \cdot (x - 2) & = (a\,x^2 + b\,x + c)\cdot (x - 2) = a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c = \\ |
& = a\,x^3 + (b - 2\,a)\,x^2 + (c - 2\,b)\,x - 2\,c = \\ | & = a\,x^3 + (b - 2\,a)\,x^2 + (c - 2\,b)\,x - 2\,c = \\ | ||
& = a \cdot x^3 + (b - 2\,a) \cdot x^2 + (c - 2\,b) \cdot x - 2\,c \cdot x^0 \\ | & = a \cdot x^3 + (b - 2\,a) \cdot x^2 + (c - 2\,b) \cdot x - 2\,c \cdot x^0 \\ | ||
| Rad 161: | Rad 164: | ||
Jämförelse av koefficienterna till <math> x^3 </math>-termen ger: | Jämförelse av koefficienterna till <math> x^3 </math>-termen ger: | ||
| − | + | ::<math>\begin{align} a & = 1 | |
\end{align} </math> | \end{align} </math> | ||
Jämförelse av koefficienterna till <math> x^2 </math>-termen ger: | Jämförelse av koefficienterna till <math> x^2 </math>-termen ger: | ||
| − | + | ::<math>\begin{align} b - 2\, a & = 4 \\ | |
b - 2\cdot 1 & = 4 \\ | b - 2\cdot 1 & = 4 \\ | ||
b - 2 & = 4 \\ | b - 2 & = 4 \\ | ||
| Rad 174: | Rad 177: | ||
Jämförelse av koefficienterna till <math> x^1 </math>-termen ger: | Jämförelse av koefficienterna till <math> x^1 </math>-termen ger: | ||
| − | + | ::<math>\begin{align} c - 2\, b & = 1 \\ | |
c - 2\cdot 6 & = 1 \\ | c - 2\cdot 6 & = 1 \\ | ||
c - 12 & = 1 \\ | c - 12 & = 1 \\ | ||
| Rad 182: | Rad 185: | ||
Jämförelse av koefficienterna till <math> x^0 </math>-termen bekräftar värdet på c: | Jämförelse av koefficienterna till <math> x^0 </math>-termen bekräftar värdet på c: | ||
| − | : | + | ::<math>\begin{align} - 2\,c & = - 26 \\ |
c & = 13 \\ | c & = 13 \\ | ||
\end{align} </math> | \end{align} </math> | ||
| Rad 189: | Rad 192: | ||
<math> Q(x) = x^2 + 6 \, x + 13 </math> | <math> Q(x) = x^2 + 6 \, x + 13 </math> | ||
| + | |||
| + | |||
[[Matte:Copyrights|Copyright]] © 2011-2014 Taifun Alishenas. All Rights Reserved. | [[Matte:Copyrights|Copyright]] © 2011-2014 Taifun Alishenas. All Rights Reserved. | ||
Versionen från 30 juli 2014 kl. 12.03
| Repetition: Algebra | Teori | Övningar | Fördjupning | Nästa avsnitt --> |
Lektion 2 Polynom: Fördjupning
Innehåll
Polynomfunktioner
När ett polynom tilldelas en annan variabel, säg \( y\, \) ger det upphov till en speciell typ av funktion, kallad polynomfunktion. Närmare bestämt är polynomfunktioner en generalisering samt utvidgning av de funktionstyper vi sysslat hittills med. I Matte 1-kursen hade vi bara linjära eller 1:a gradsfunktioner av typ:
- \[ y = 4\,x + 12 \]
Till höger om likhetstecknet står ett polynom där \( x\, \) förekommer som 1:a gradspotens dvs med exponenten 1. Därför kallas \( 4 x\, \) polynomets linjära term. Dess koefficient är \( 4\, \). Polynomets konstanta term är \( 12\, \). Grafen till denna 1:a gradsfunktion är en rät linje. I Matte 2-kursen gick vi ett steg vidare och sysslade med 2:a gradsfunktioner av typ:
- \[ y = 3\,x^2 + 5\,x - 16 \]
Här är graden 2. Koefficienten till den kvadratiska termen \( 3 x^2\, \) är \( 3\, \). Koefficienten till den linjära termen \( 5 x\, \) är \( 5\, \). Och koefficienten till den konstanta termen \( -16 x^0\, \) är \( -16\, \). Grafen till denna 2:a gradsfunktion är en parabel. Dessa funktioner kallas polynomfunktioner därför att uttrycken till höger om likhetstecken är polynom, eftersom de är summor av termer som uppfyller de villkor som vi införde för \( n\, \) - nämligen att vara ett positivt heltal eller 0. Vi har alltså i Matte 1 och 2 sysslat med polynomfunktioner där n var 0, 1 eller 2, men inte högre.
I Matte 3-kursen ska vi nu lära oss att hantera även polynom av högre grad än 2. Vi tar som exempel följande 4:e gradspolynomfunktion samt graf:
- \[ y = x^4 - 29\;x^2 + 100 \]
Som man ser är grafen mer komplicerad än en parabel. Den har fler minima, maxima och nollställen. Funktionens nollställen är identiska med lösningarna till 4:e gradsekvationen \( x^4 - 29\;x^2 + 100 = 0 \).
Polynomfunktioner av högre grad
Funktionen ovan \( y = x^4 - 29\;x^2 + 100 \) var redan ett exempel på en polynomfunktion av högre grad. Ett polynoms grad är ett mått på dess kompexitet. För att se hur kompexiteten växer med graden (från 0 till 5) ska vi titta på följande sex polynom:
Polynomen \(U_n(x)\,\) bildar en följd av polynom där varje polynom har ett index \(n\,\) som samtidigt är polynomets grad.
De nedsänkta indexen \(_0,\,_1,\,_2,\,_3,\,_4,\,_5\) i beteckningarna \(U_0, U_1, U_2, U_3, U_4, U_5\,\) används här både för att relatera indexet till polynomets grad och kunna sedan (några rader längre fram) skriva en formel för dessa polynom som kommer att visa hur de hänger ihop som en familj.
Här följer graferna till polynomen ovan ritade i samma koordinatsystem. De visar att kurvorna svänger oftare och får fler maxima/minima ju högre deras grad är:
Dessa polynom heter Chebyshevpolynom av 2:a slag efter den ryske matematikern Chebyshev som presenterade dem 1854. De är relaterade till varandra med följande formel, kallad rekursionsformel:
- \[ U_n(x) = 2\,x\,\cdot\,U_{n-1}(x)\,-\,U_{n-2}(x) \qquad\qquad n = 2, 3, ... \]
- \[ U_0(x) = 1, \quad U_1(x) = 2\,x \]
Denna formel ger oss möjligheten att ta fram Chebyshevpolynomen rekursivt (successivt), dvs vi kan ställa upp ett polynom med hjälp av de två föregående. De första två Chebyshevpolynomen \(U_0, U_1\,\) är explicit angivna (i den andra raden). Det tredje Chebyshevpolynomet \(U_2\,\) får man genom att sätta in \(U_0, U_1\,\) i högerledet av rekursionsformeln (i den första raden). Det fjärde Chebyshevpolynomet \(U_3\,\) får man genom att sätta in \(U_1, U_2\,\) i högerledet osv. Det finns oändligt många Chebyshevpolynom. I princip kan man få dem alla med rekursionsformeln utgående från de två första. Man kan säga att följden av Chebyshevpolynomen definieras och genereras av rekursionsformeln ovan. Låt oss börja med att ställa upp det tredje (OBS! n = 2) med hjälp av de två första (n = 0 och 1):
- \[ \displaystyle U_0(x) = \underline{1} \]
- \[ U_1(x) = \underline{2\,x} \]
För n = 2 ger rekursionsformeln:
- \[ U_2(x) = 2\,x\,\cdot\,U_1(x)\,-\,U_0(x) = 2\,x\,\cdot\,2\,x\,-\,1 = \underline{4\,x^2\,-\,1} \]
Sedan kan vi få fram \( U_3(x) \) genom att att sätta in n = 3 i rekursionsformeln:
- \[ U_3(x) = 2\,x\,\cdot\;U_2(x)\,-\,U_1(x) = 2\,x\,\cdot\,(4\,x^2\,-\,1)\,-\,2\,x = 8\,x^3\,-\,2\,x\,-\,2\,x = \underline{8\,x^3\,-\,4\,x} \]
För n = 4 ger rekursionsformeln \( U_4(x) \) osv.:
- \[ U_4(x) = 2\,x\,\cdot\,U_3(x)\,-\,U_2(x) = 2\,x\,\cdot\,(8\,x^3\,-\,4\,x)\,-\,(4\,x^2\,-\,1) = 16\,x^4\,-\,8\,x^2\,-\,4\,x^2\,+\,1 = \underline{16\,x^4\,-\,12\,x^2\,+\,1} \]
Så här kan man fortsätta för att få fram alla Chebyshevpolynom. Förfarandet är rekursivt eftersom formeln används för att ställa upp ett polynom från de två föregående.
Jämförelse av koefficienter
Jämförelse av koefficienter är en teknik eller en metod som vi kommer att använda för att lösa högre gradsekvationer genom att faktorisera polynom av högre grad än 2, se övningarna 10 och 11.
Metoden bygger på begreppet likhet mellan polynom. Därför ska vi börja med att definiera likhet mellan polynom.
Definition:
Två polynom:
- \[ P(x) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + \quad \ldots \quad + a_1 \cdot x + a_0 \]
och
- \[ Q(x) = b_n \cdot x^n + b_{n-1} \cdot x^{n-1} + \quad \ldots \quad + b_1 \cdot x + b_0 \]
är lika med varandra om de har samma grad och om alla deras motsvarande koefficienter, dvs de som tillhör termer av samma grad, överensstämmer, närmare bestämt om:
- \[ a_n = b_n, \quad a_{n-1} = b_{n-1}, \quad \ldots \quad a_1 = b_1, \quad a_0 = b_0 \]
Exempel 1
Två polynom är givna:
- \[ P(x) = a \cdot x + 2\,a + b \]
- \[ Q(x) = 2\,x + 1\!\, \].
Låt \( a\, \) och \( b\, \) vara konstanter medan \( x\, \) är polynomens oberoende variabel.
För vilka värden på \( a\, \) och \( b\, \) är de två polymen lika med varandra?
Vi skriver \( P(x),\, \) och \( Q(x)\, \) så att vi lättare kan se motsvarande koefficienter:
- \[ P(x) = a \cdot x^1 + (2\,a + b) \cdot x^0 \]
- \[ Q(x) = 2 \cdot x^1 + \quad\;\; 1 \quad\;\; \cdot x^0 \]
Jämförelse av koefficienterna till \( x^1\, \) leder till:
- \[ a = 2\,\]
Jämförelse av koefficienterna till \( x^0 \,\) leder till:
- \[ 2\,a + b = 1\!\,\]
Sätter man in \( a = 2\, \) i denna relation får man \( b = -3\, \).
Polynomen \( P(x)\, \) och \( Q(x)\, \) är lika med varandra för:
- \[ a = 2\, \]
- \[ b = -3\, \]
Exempel 2
Problem: Följande 3:e gradspolynom är givet\[ P(x) = x^3 + 4\,x^2 + x - 26 \]
Hitta ett 2:a gradspolynom \( Q(x)\, \) så att:
- \[ Q(x)\cdot (x-2) = P(x) \]
Svar:
- \[ Q(x) = x^2 + 6 \, x + 13 \]
Lösning:
Det 2:a gradspolynomet \( Q(x)\, \) kan skrivas så här\[ Q(x) = a\,x^2 + b\,x + c \]
Vi bestämmer koefficienterna \( a\, , \, b\, \) och \( c\, \) så att \( Q(x)\cdot (x-2) = P(x) \)
- \[\begin{align} Q(x) \cdot (x - 2) & = (a\,x^2 + b\,x + c)\cdot (x - 2) = a\,x^3 - 2\,a\,x^2 + b\,x^2 - 2\,b\,x + c\,x - 2\,c = \\ & = a\,x^3 + (b - 2\,a)\,x^2 + (c - 2\,b)\,x - 2\,c = \\ & = a \cdot x^3 + (b - 2\,a) \cdot x^2 + (c - 2\,b) \cdot x - 2\,c \cdot x^0 \\ P(x) & = 1 \cdot x^3 + \quad\;\; 4 \quad\;\; \cdot x^2 + \quad\;\; 1 \quad\;\; \cdot x - 26 \cdot x^0 \end{align} \]
Jämförelse av koefficienterna till \( x^3 \)-termen ger:
- \[\begin{align} a & = 1 \end{align} \]
Jämförelse av koefficienterna till \( x^2 \)-termen ger:
- \[\begin{align} b - 2\, a & = 4 \\ b - 2\cdot 1 & = 4 \\ b - 2 & = 4 \\ b & = 6 \\ \end{align} \]
Jämförelse av koefficienterna till \( x^1 \)-termen ger:
- \[\begin{align} c - 2\, b & = 1 \\ c - 2\cdot 6 & = 1 \\ c - 12 & = 1 \\ c & = 13 \\ \end{align} \]
Jämförelse av koefficienterna till \( x^0 \)-termen bekräftar värdet på c:
- \[\begin{align} - 2\,c & = - 26 \\ c & = 13 \\ \end{align} \]
Vi får \( a = 1\, , \, b = 6\, \) och \( c = 13\, \) och därmed\[ Q(x) = x^2 + 6 \, x + 13 \]
Copyright © 2011-2014 Taifun Alishenas. All Rights Reserved.